Question

Three particles, each of mass M, are situated at the vertices of an equilateral triangle of side ‘a’. The only forces acting on the particles are their mutual gravitational forces. It is desired that each particle moves in a circle while maintaining their original separation ‘a’. The initial velocity that should be given to each particle and time period of circular motion are respectively.
A. $\sqrt {\dfrac{{2GM}}{a}} ,2\pi \sqrt {\dfrac{{{a^3}}}{{3GM}}} $
B. $\sqrt {\dfrac{{GM}}{a}} ,\dfrac{1}{{2\pi }}\sqrt {\dfrac{{3GM}}{{{a^3}}}} $
C. $\sqrt {\dfrac{{GM}}{a}} ,2\pi \sqrt {\dfrac{{{a^3}}}{{3GM}}} $
D. $\sqrt {\dfrac{{GM}}{{3a}}} ,2\pi \sqrt {\dfrac{{{a^3}}}{{3GM}}} $

Answer 1

Hint: Net gravitational force acting on each particle should balance the centripetal force to maintain the original distance of separation during the circular motion

Complete answer:
According to Newton’s law of Gravitation, gravitational force acting between two masses is directly proportional to the product of their masses and inversely proportional to the square of distance between the centres of the two masses. In the given problem, the three masses are same as $M$ and are positioned on the vertex of an equilateral triangle ABC of side $a$ as follows:

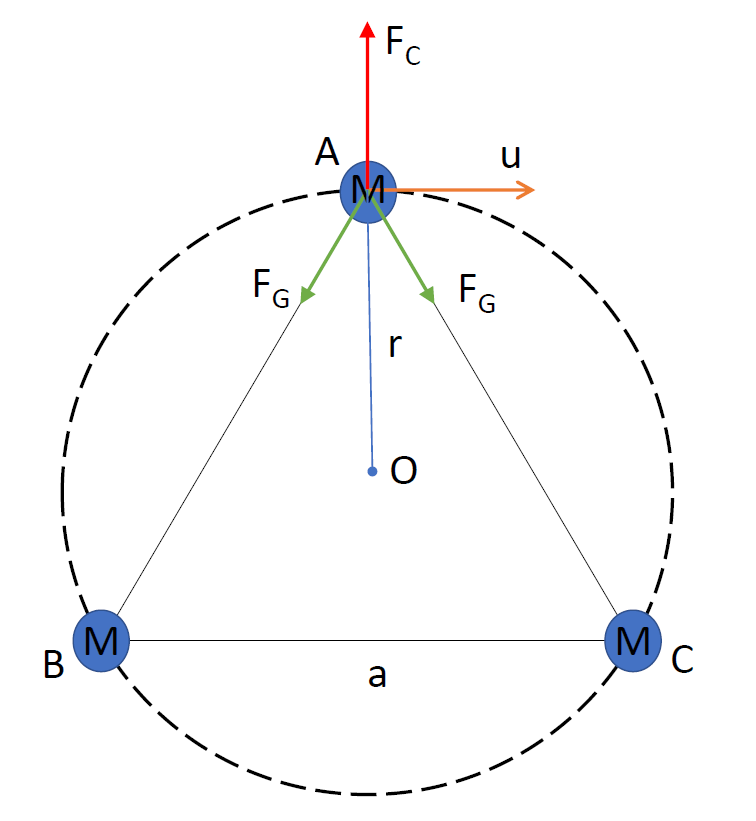
Let O be the centre and $r$ be the radius of the circular motion and $u$ be the velocity of the particles along the circle. Consider the force balance for particles at A.
Outward centripetal force on the particle is given by following expression:
${F_C} = \dfrac{{M{u^2}}}{r}$ (1)
Gravitation force in the direction given in the above diagram based on Newton’s law discussed earlier is given as follows. Consider force on A due to C.
${F_G} = \dfrac{{G{M^2}}}{{{a^2}}}$ (2)
Since the mass at B is also same, the magnitude of the gravitational force is same but directed as shown in above direction, i.e. from A to B. Resultant of two vectors p, q is given by
$R = \sqrt {{p^2} + {q^2} + 2pq\cos \theta } $
Here, both vectors are gravitational forces separated by angle, $\theta = 60$. Since both their magnitudes are the same they will be directed toward the centre in the direction opposite to centripetal force as shown in the diagram. This is also because we have positioned the particles at the vertex of the equilateral triangle. So the resultant gravitational force is given as:
$\begin{gathered}
   \Rightarrow R = \sqrt {{{\left( {\dfrac{{G{M^2}}}{{{a^2}}}} \right)}^2} + {{\left( {\dfrac{{G{M^2}}}{{{a^2}}}} \right)}^2} + 2\left( {\dfrac{{G{M^2}}}{{{a^2}}}} \right)\left( {\dfrac{{G{M^2}}}{{{a^2}}}} \right)\cos 60} \\
   \Rightarrow R = \sqrt 3 \dfrac{{G{M^2}}}{{{a^2}}} \\
\end{gathered} $ (3)
Now, for maintaining the circular motion and also the distance the centripetal force in (1) should balance the resultant force given in (3). We get the following relation,
$ \Rightarrow R = {F_C}$
$ \Rightarrow \sqrt 3 \dfrac{{G{M^2}}}{{{a^2}}} = \dfrac{{M{u^2}}}{r}$
$ \Rightarrow {u^2} = \dfrac{{\sqrt 3 rGM}}{{{a^2}}}$
Since the circle covers the equilateral triangle, the radius of the circle and the side of the equilateral triangle as follows:
$\begin{gathered}
   \Rightarrow \dfrac{{\left( {\dfrac{a}{2}} \right)}}{r} = \cos 30 = \dfrac{{\sqrt 3 }}{2} \\
   \Rightarrow a = \sqrt 3 r \\
\end{gathered} $.
The line joining the centre to the vertex becomes the angle bisector at vertex. So we have 30 degrees for the above cosine term.
Substituting this in the last velocity relation,
$ \Rightarrow u = \sqrt {\dfrac{{GM}}{a}} $ (4)
To find the time period of the motion, we need to find the time the particle takes to complete one revolution around the centre. Distance covered in one revolution is equal to the circumference of the circle $ = 2\pi r$ and let $T$ be the time period.
$ \Rightarrow u = \dfrac{{2\pi r}}{T} = \dfrac{{2\pi a}}{{\sqrt 3 T}}$. Using the relation between $a$ and $r$.
$\begin{gathered}
   \Rightarrow \sqrt {\dfrac{{GM}}{a}} = \dfrac{{2\pi a}}{{\sqrt 3 T}} \\
   \Rightarrow T = 2\pi \sqrt {\dfrac{{{a^3}}}{{3GM}}} \\
\end{gathered} $ (5)
Comparing (4) and (5) with the options, we see that option C is the correct option.
Note: While simplifying the expressions focus on bringing the terms with parameters used in the options. Like the final expressions can be written in terms of $r$ instead of $a$.