Question

Three particles. each of mass m gram, are situated at the vertices of an equilateral triangle ABC of side l cm (as shown in the figure). The moment of inertia of the system about a line AX perpendicular to AB and in the plane of ABC, in gram-cm2 units will \[c{{m}^{2}}\]
(A) \[2m{{l}^{2}}\]
(B) \[\dfrac{5}{4}m{{l}^{2}}\]
(C) \[\dfrac{3}{2}m{{l}^{2}}\]
(D) \[\dfrac{3}{4}m{{l}^{2}}\]

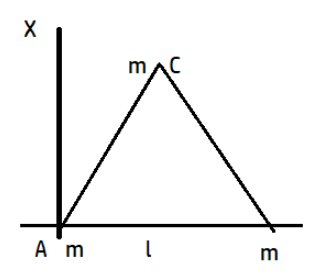
Answer 1

Hint: We are given with three particles each of mass m, situated at the three edges of the equilateral triangle. The one vertex of the equilateral triangle sits at the origin of the triangle. We have to find the moment of inertia around the perpendicular axis.

Complete step by step answer:

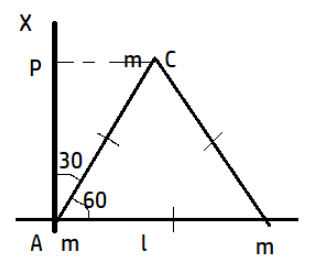
We can find the moment of inertia, by using the formula \[{{m}_{a}}r_{a}^{2}+{{m}_{b}}r_{b}^{2}+{{m}_{c}}r_{c}^{2}\]. The question asks the value of the moment of inertia about a particular axis that means we have to only calculate the x component of the moment of inertia. We need to find the x coordinates of the three particles.
For mass situated at A- (0)
For mass situated at B- (l)
For mass situated at C- using trigonometry in right-angled triangle CPA,
\[\begin{align}
& \sin 30=\dfrac{PC}{AC} \\
&\Rightarrow \dfrac{1}{2}=\dfrac{PC}{l} \\
&\Rightarrow PC=\dfrac{l}{2} \\
\end{align}\]
So, For mass situated at C-(l/2)
Thus, the moment of inertia(I) is,
\[\begin{align}
&\Rightarrow I =m(0)_{{}}^{2}+m{{l}^{2}}+m{{(\dfrac{l}{2})}^{2}} \\
&\Rightarrow I =m{{l}^{2}}+m{{l}^{2}}+\dfrac{m{{l}^{2}}}{4} \\
&\therefore I =\dfrac{5}{4}m{{l}^{2}} \\
\end{align}\]
Hence,option (B) is the correct answer.

Note:In this problem, the coordinates were not mentioned, since the points A and B lie on the x-axis, the x coordinates of A and B were the distance of the points A and B from the origin respectively. For point C, the simplest method was to use trigonometric ratios since the right-angled triangle was involved.