Question

Three sets of English, Hindi and Mathematics books have to be stacked in such a way that all the books are stored topic-wise and the height of each stack is the same. The number of English books is 96, the number of Hindi books is 240 and the number of Mathematics books is 336. Assuming that the books are of the same thickness, determine the number of stacks of English, Hindi and Mathematics books.

Answer 1

Hint: In order to solve this question, we should know the concept of the highest common factor. The highest common factor or HCF of the given number is the greatest number which can divide all of them. So, to solve this question, we will first find the HCF by long division method to find the number of books in each stack and then we will divide it with a number of books to get the number of stacks.

Complete step-by-step answer:
In this question, we have been given that there are 96 English, 240 Hindi, and 336 Mathematics books and we are asked to stack them. To solve this question, we will take the HCF of 96, 240, and 336 by long division method. And we know that in the long division method, for HCF, we divide the largest number by the smallest number and then take the divisor as new dividend and remainder as the new divisor and we continue till the remainder becomes zero and then consider the last divisor as HCF.
So, we will first apply the long division method for 336 and 240. So, we can write

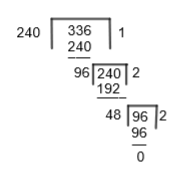
Hence, we can say 48 is the HCF of 240 and 336. Now, to find the HCF of 96, 240, and 336, we will consider 48 as the divisor and 96 as a dividend, and then we will apply the long division method. So, we get,

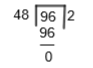
Hence, we can say 48 is the HCF of 96, 240, and 336. Or we can say there are 48 books in each stack to make the height of each stack equal.
Now, to find the number of stacks of each subject, we will divide the number of books of that subject by the number of books in each stack, i.e. 48. So, we get,
Number of the stack of English books \[=\dfrac{96}{48}=2\]
Number of the stack of Hindi books \[=\dfrac{240}{48}=5\]
Number of the stack of Mathematics books \[=\dfrac{336}{48}=7\]
Hence, we can say there are 2 stacks of English books, 5 stacks of Hindi books, and 7 stacks of Mathematics books.

Note: While solving this question, we need to remember that whenever we have to divide a large number of items into smaller parts so that they can be stacked of an equal number we take their HCF which is the greatest number which can divide all the given numbers. We can also find the HCF of the given number by writing the factor of the numbers like
\[96={{2}^{5}}\times 3;240={{2}^{4}}\times 3\times 5;336={{2}^{4}}\times 3\times 7\]
Hence, we can say that all the numbers are divisible by \[{{2}^{4}}\times 3=48\]. Hence, 48 is the HCF of 96, 240, 336.