Question

Three uniform spheres of mass 2.00 kg, 4.00 kg and 6.00 kg are placed at the corners of a right triangle as in the figure. Assuming the spheres are isolated from the rest of the universe, choose the correct statements from the following.

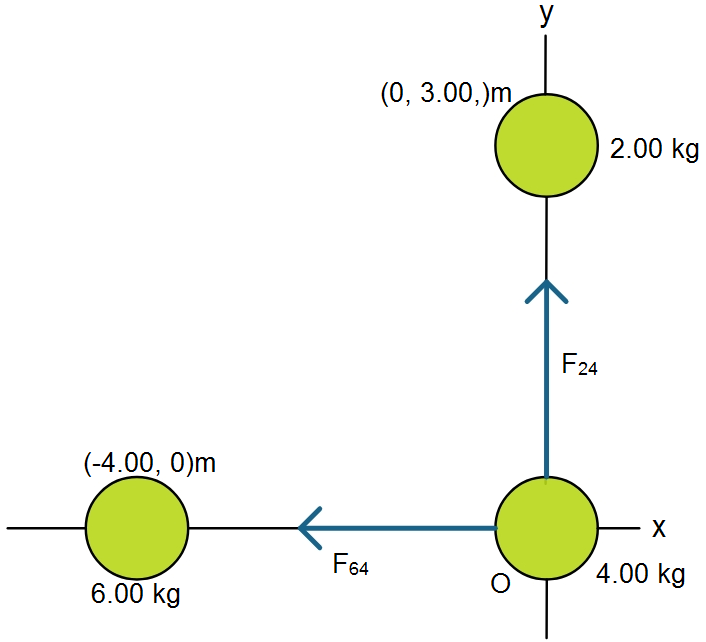
(A) The resultant gravitational force on the 4.00 kg object is (-100$\hat{i}$ + 59.3$\hat{j}$) pN
(B) There resultant gravitational force on the 4.00 kg object is (-50$\hat{i}$ + 59.3$\hat{j}$) pN
(C) If the 2.00 kg object and the 6.00 kg object are interchanged the magnitude of the resultant gravitational force on the 4.00 kg object remains the same.
(D) If the 2.00 kg object and the 4.00 kg object are interchanged then the resultant gravitational force on the 2.00 kg object is (-50$\hat{i}$ + 59.3$\hat{j}$) pN.

Answer 1

Hint: The magnitude of the vectors displayed in the question diagram can be determined using the usual gravitational force expression. The resultant can be calculated using parallelogram law of vector addition.
Formula used:
Between any two masses, the force of gravity experienced is written as:
$F_{21} = F_{12} = G \dfrac{m_1 m_2}{r^2}$
(in magnitude).

Complete answer:
We deal with all the options one by one;
(A). The resultant force on 4 kg mass is the vector sum of the forces between 2 kg and 4 kg mass and 6 kg and 4 kg mass.
First, let us write the magnitude of force between 6 kg and 4 kg:
$F_{64} = 6.67 \times 10^{-11} \times \dfrac{6 \times 4}{4^2} = 1.001 \times 10^{-10}$ N = 100 pN (approx.)
Similarly, between 2 kg and 4 kg mass we have:
$F_{24} = 6.67 \times 10^{-11} \times \dfrac{2 \times 4}{3^2} = 5.932 \times 10^{-11}$ N = 59.3 pN (approx.)

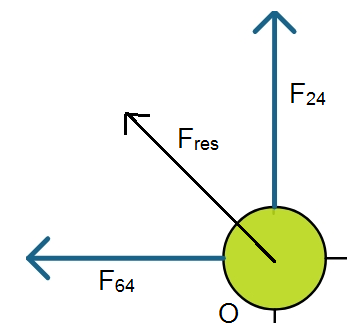
We apply parallelogram law of vector addition so that the resultant we get is

$F_{res} = -100\hat{i} + 59.3 \hat{j}$

Therefore option (A) is a correct statement.

(B) Now, as we already established (A) is correct this clearly means that the statement (B) has to be incorrect.

(C). This statement is also incorrect because the magnitude of the gravitational force not only depends on the masses but also depends on the distance of separation. If we change the position of the masses, the resultant will not remain the same.

(D). The force between 2 kg and 4 kg will still have the same magnitude as we had previously, which was 59.3 pN.
The magnitude of force between 2 kg and 6 kg will be:
$F_{62} = 6.67 \times 10^{-11} \times \dfrac{6 \times 2}{4^2} = 5.005 \times 10^{-11}$ N = 50 pN (approx.).
Therefore the statement in option (D) is also correct.

So, the correct answer is “Option A and D”.

Note:
The vector addition has to be performed keeping in mind the positive or negative directions on the x or y axis. As on the x axis, our force vector points in negative x direction, the force will be taken as negative. Along the y direction, the force is along a positive y direction, so it is taken positively. Mind that even when the force would have depicted towards the negative side of x axis, but if the arrow of the vector points towards +x direction, the force had to be taken positively.