
Three vertices of a rhombus taken in order are
Answer
436.2k+ views
Hint: Here, in the given question, the three vertices of a rhombus are given and we are asked to find the fourth one. As we know that, rhombus has a special property that the diagonals of rhombus bisect each other. We will use this property and midpoint formula to get the required vertex of a rhombus.
Formula used:
Midpoint formula: If
Complete step-by-step solution:
Given, three vertices of rhombus
Let the fourth vertex be
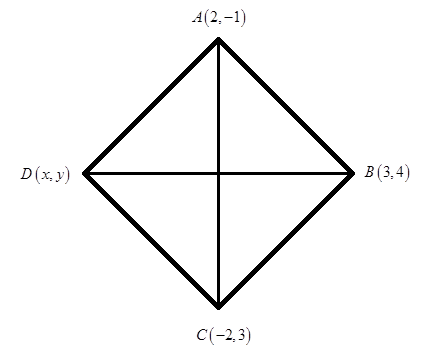
Now, we have,
We know that the rhombus has a property that the diagonals of rhombus bisect each other perpendicularly. In the given rhombus,
If diagonal bisects each other, then the midpoint of the diagonals should be the same.
Using Midpoint formula,
Coordinates of midpoint of
=
Coordinates of midpoint of
Since, midpoint of
Hence, the fourth vertex of the given rhombus is
Note: Alternatively, this question can also be solved using distance formula between two points.
Some properties of rhombus are:
> All the four sides of a rhombus are equal to one another.
> Opposite sides of a rhombus are parallel to each other.
> Opposite angles of rhombus are equal.
> Diagonals of a rhombus bisect each other perpendicularly.
> The adjacent angles of rhombus are supplementary.
using this property we can solve the problem easily.
Formula used:
Midpoint formula: If
Complete step-by-step solution:
Given, three vertices of rhombus
Let the fourth vertex be

Now, we have,
We know that the rhombus has a property that the diagonals of rhombus bisect each other perpendicularly. In the given rhombus,
If diagonal bisects each other, then the midpoint of the diagonals should be the same.
Using Midpoint formula,
Coordinates of midpoint of
=
Coordinates of midpoint of
Since, midpoint of
Hence, the fourth vertex of the given rhombus is
Note: Alternatively, this question can also be solved using distance formula between two points.
Some properties of rhombus are:
> All the four sides of a rhombus are equal to one another.
> Opposite sides of a rhombus are parallel to each other.
> Opposite angles of rhombus are equal.
> Diagonals of a rhombus bisect each other perpendicularly.
> The adjacent angles of rhombus are supplementary.
using this property we can solve the problem easily.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Questions & Answers - Ask your doubts

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 Science: Engaging Questions & Answers for Success

Trending doubts
A boat goes 24 km upstream and 28 km downstream in class 10 maths CBSE

Why is there a time difference of about 5 hours between class 10 social science CBSE

The Equation xxx + 2 is Satisfied when x is Equal to Class 10 Maths

What is the full form of POSCO class 10 social science CBSE

Change the following sentences into negative and interrogative class 10 english CBSE

How do you prove that the diagonals of a rectangle class 10 maths CBSE




