Question

Three-point masses each of mass m are placed at the corners of an equilateral triangle of side a. The moment of inertia of the system about, an axis along one side of the triangle is
(a) $2m{{a}^{2}}$
(b) $m{{a}^{2}}$
(c) $\dfrac{3}{4}m{{a}^{2}}$
(d) $\dfrac{3}{2}m{{a}^{2}}$

Answer 1

Hint: To find the moment of inertia of a system about an axis along any one side of the triangle we will consider the axis passing through any one side of the triangle. Then on the basis of that we will find the moment of inertia of masses considering their perpendicular distance from the axis and then we will find the answer using formula $I=m{{r}^{2}}$.

Formula used: $I=m{{r}^{2}}$

Complete step-by-step answer:
In question it is given that three-point masses each of mass m are placed at the corners of an equilateral triangle of side a. So, first of all we will draw the figure for our simplicity.

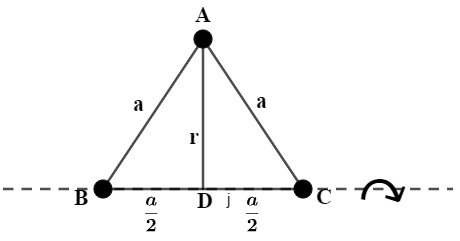
Now, we will consider that axis passes through the side BC of the triangle ABC. Now, we know that the moment of inertia is given by the formula,
$I=m{{r}^{2}}$
Where, m is mass of the body and r is the perpendicular distance of the mass from the axis.
Now, on the basis of the formula we will find the perpendicular distance of masses from the axis. Now, we know that the masses which lie on the axis itself do not have perpendicular distances. So, now we will consider the mass lying at point A of the triangle.
Now, from the figure it can be seen that we can consider $\Delta ADC$, to find the perpendicular distance i.e. AD.
Let’s consider AD as r, AC is $a$ and DC is $\dfrac{a}{2}$. By applying Pythagoras theorem, we will find AD, which can be given mathematically as,
$A{{C}^{2}}=A{{D}^{2}}+D{{C}^{2}}$
$\Rightarrow {{a}^{2}}={{r}^{2}}+{{\left( \dfrac{a}{2} \right)}^{2}}$
$\Rightarrow {{a}^{2}}-\dfrac{{{a}^{2}}}{4}={{r}^{2}}$
$\Rightarrow {{r}^{2}}=\dfrac{4{{a}^{2}}-{{a}^{2}}}{4}=\dfrac{3{{a}^{2}}}{4}$
$\Rightarrow {{r}^{2}}=\dfrac{3{{a}^{2}}}{4}$
Now, substituting the value of ${{r}^{2}}$ in expression (i) we will find the moment of inertia along the axis passing through BC. This can be given mathematically as,
$I=m\dfrac{3{{a}^{2}}}{4}\Rightarrow I=\dfrac{3m{{a}^{2}}}{4}$
Thus, we can say that the moment of inertia of the system, an axis along one side of the triangle is$\dfrac{3}{4}m{{a}^{2}}$.
Hence, option (c) is correct.

Note: Students can also consider the axis passing through side AC or side AB of the triangle, as it will only change the terms in the equation but the final answer will remain the same. Students should not forget to take Pythagoras theorem for finding the perpendicular distance of mass m at any side otherwise he won’t be able to find the answer.