
To draw a pair of tangents to a circle which are inclined to each other at an angle of
A.
B.
C.
D.
Answer
486.3k+ views
Hint: Draw a rough diagram of a circle with a pair of tangents to the circle drawn from a single point. Join the radius at the points of contact of the tangent with the circle. Assume the angle between the two radii as
Complete step by step answer:
Let us draw the diagram according to the situation given in the question.
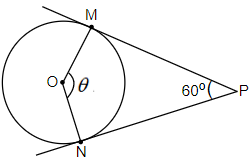
In the above figure, we have considered a circle with centre O. Tangents are drawn from point P, which are PM and PN. We can see that the points of contact of tangent PM and PN with the circle are M and N respectively.
Now, we have joined OM and ON. So, clearly OM and ON are the radius of the circle. We have assumed the angle between these radii as
Here, we know that, radius of a circle is perpendicular to the tangent at the point of contact. Therefore, OM is perpendicular to PM and ON is perpendicular to PN.
Clearly, we can see that OMNP is a quadrilateral and we know that, sum of all interior angles is equal to
Substituting the values of
Hence, option C is the correct answer.
Note:
One may note that we must draw a rough diagram before solving the question as it will help us to visualize the situation more effectively. Here, we have applied the property of sum of all interior angles of quadrilateral because we knew the values of three angles and there was only one unknown one.
Complete step by step answer:
Let us draw the diagram according to the situation given in the question.

In the above figure, we have considered a circle with centre O. Tangents are drawn from point P, which are PM and PN. We can see that the points of contact of tangent PM and PN with the circle are M and N respectively.
Now, we have joined OM and ON. So, clearly OM and ON are the radius of the circle. We have assumed the angle between these radii as
Here, we know that, radius of a circle is perpendicular to the tangent at the point of contact. Therefore, OM is perpendicular to PM and ON is perpendicular to PN.
Clearly, we can see that OMNP is a quadrilateral and we know that, sum of all interior angles is equal to
Substituting the values of
Hence, option C is the correct answer.
Note:
One may note that we must draw a rough diagram before solving the question as it will help us to visualize the situation more effectively. Here, we have applied the property of sum of all interior angles of quadrilateral because we knew the values of three angles and there was only one unknown one.
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

What are Quantum numbers Explain the quantum number class 11 chemistry CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE




