Question

To go from town A to town B a plane must fly about 1780km at an angle of 300 west of north how far west of A is B?
A) 1542km
B) 1452km
C) 1254km
D) 890km

Answer 1

Hint
In this equation first of all we draw the diagram for the given condition. After obtaining the diagram we can find the remaining angles then we can resolve the components in terms of $\sin \theta $ and $\cos \theta $then applying the formula i.e. $\sin \theta = \dfrac{{perpendicular}}{{hypotenuse}}$ and $\cos \theta = \dfrac{{base}}{{hypotenuse}}$. We can find the value of base, perpendicular and hypotenuse from the diagram and after substituting the values we get the required value of AD.

Complete step by step answer
First of all, we draw the diagram by using the given conditions. Firstly, mark the directions north, south, east and west. After that let a plane is flying at an angle of 300 west of north then mark this angle on diagram as ${\theta _1} = {30^0}$

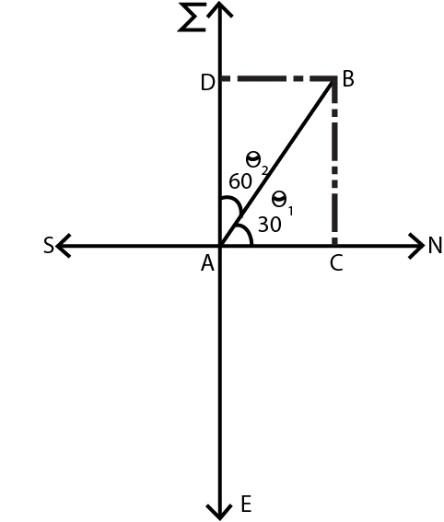
Now we have to find how far west of A is B i.e. we have to find the value of AD as shown in diagram.
Now as the angle between north and west direction is 900 and it is given that ${\theta _1} = {30^0}$ then we can find the value of $θ_2$ i.e. ${\theta _2} = {90^0} - {\theta _1} = {90^0} - {30^0} = {60^0}$
Now it is also given that the distance of AB = 1780km
We have to find the value of AD.
From the diagram, hypotenuse is given and we have to find the value of base with respect to the angle $θ_2$, therefore we will use the formula of i.e. $\cos \theta = \dfrac{{base}}{{hypotenuse}}$
As hypotenuse = AB = 1780km
Angle ${\theta _2} = {60^0}$
On substituting the values, we get
$ \Rightarrow \cos 60 = \dfrac{{AD}}{{1780}}$
As $\cos 60 = \dfrac{1}{2}$then above equation become
$ \Rightarrow AD = \dfrac{1}{2} \times 1780$
$ \Rightarrow AD = 890km$
Hence, option (D) is correct.

Note
Here, care must be taken for making the diagram and it must be noticed that we can solve this question by using the angle 300.
For this first resolve the components of angle 300 i.e. $AC = AB\cos 30$ and $AD = AB\sin 30$
As we also know that $\sin 30 = \dfrac{1}{2}$then $AD = 1780 \times \dfrac{1}{2} = 890km$. Which is same as above
Here, care must be taken for observing the question for example if instead of how far west of A is B, he asked how far north of A is B then we need to find the value of AC i.e. $AC = AB\cos 30$, on substituting the values we get $AC = 1780 \times \dfrac{{\sqrt 3 }}{2} \approx 1542km$