Question

TP and TQ are tangents to parabola \[{{y}^{2}}=4ax\] and normals at P and Q intersect at a point R on the curve. The locus of the center of the circle circumscribing \[\Delta TPQ\] is a parabola whose
(a) vertex is (1, 0)
(b) foot of directrix is \[\left( \dfrac{7}{8},0 \right)\]
(c) length of latus – rectum is \[\dfrac{1}{4}\]
(d) focus is \[\left( \dfrac{9}{8},0 \right)\]

Answer 1

Hint: Prove that the center of the circle circumscribing is simplified to \[{{y}^{2}}=\dfrac{x-1}{2}\], where (x, y) are the coordinates of the center.

Complete step-by-step answer:

We know that the equation of parabola is

\[{{y}^{2}}=4ax\]

From the question, \[{{y}^{2}}=4x\], where a = 1.

Let us consider the two points as \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\].

Now, we need to find the intersection of tangents at P and Q.

Differentiate the equation of parabola,

\[\Rightarrow {{y}^{2}}=4ax\]

Therefore, \[2y.\dfrac{dy}{dx}=4a\]

\[\Rightarrow \dfrac{dy}{dx}=\dfrac{2a}{y}\]

Therefore, slope of a tangent at a given point \[\left( {{x}_{1}},{{y}_{1}} \right)\] having slope m, by point – slope form

\[y-{{y}_{1}}=m\left( x-{{x}_{1}} \right)\]

Therefore, equation of tangent

\[\Rightarrow y-{{y}_{1}}=\dfrac{2a}{{{y}_{1}}}\left( x-{{x}_{1}} \right)\]

\[{{y}_{1}}\left( y-{{y}_{1}} \right)=2ax-2a{{x}_{1}}\text{ }\left[ \because y_{1}^{2}=4a{{x}_{1}}

\right]\]

\[{{y}_{1}}y-y_{1}^{2}=2ax-2a{{x}_{1}}\]

\[\Rightarrow {{y}_{1}}y-4a{{x}_{1}}=2ax-2a{{x}_{1}}\]

\[\Rightarrow {{y}_{1}}y=2ax+2a{{x}_{1}}\]

\[\therefore y{{y}_{1}}=2a\left( x+{{x}_{1}} \right)\]

For point \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\],

Equation of tangent at \[{{t}_{1}}\],

\[\Rightarrow y\left( 2a{{t}_{1}} \right)=2a\left( x+at_{1}^{2} \right)\]

\[y{{t}_{1}}=x+at_{1}^{2}....\left( i \right)\]

Similarly at \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\]

Equation of tangent at \[{{t}_{2}}\],

\[\Rightarrow y\left( 2a{{t}_{2}} \right)=2a\left( x+at_{2}^{2} \right)\]

\[y{{t}_{2}}=x+at_{2}^{2}....\left( ii \right)\]

Now, equation (i) – equation (ii)

\[\Rightarrow y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left( t_{1}^{2}-t_{2}^{2} \right)\text{ }\left[ \because {{a}^{2}}-{{b}^{2}}=\left( a+b \right)\left( a-b \right) \right]\]

\[y\left( {{t}_{1}}-{{t}_{2}} \right)=a\left( {{t}_{1}}-{{t}_{2}} \right)\left( {{t}_{1}}+{{t}_{2}}

\right)\]

\[\Rightarrow y=a\left( {{t}_{1}}+{{t}_{2}} \right)\]

Substitute value of y in equation (i).

\[a\left( {{t}_{1}}+{{t}_{2}} \right){{t}_{1}}=x+at_{1}^{2}\]

\[at_{1}^{2}+a{{t}_{1}}{{t}_{2}}=x+at_{1}^{2}\]

\[\Rightarrow x=a{{t}_{1}}{{t}_{2}}\]

Therefore, point of intersection of tangents P and Q is \[T\left[ a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right]\].

Similarly, the point of intersection of normals drawn at \[P\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[Q\left( at_{2}^{2},2a{{t}_{2}} \right)\] is given by point R, where the coordinates of R is \[\left[ a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}}+2 \right),-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right]\]

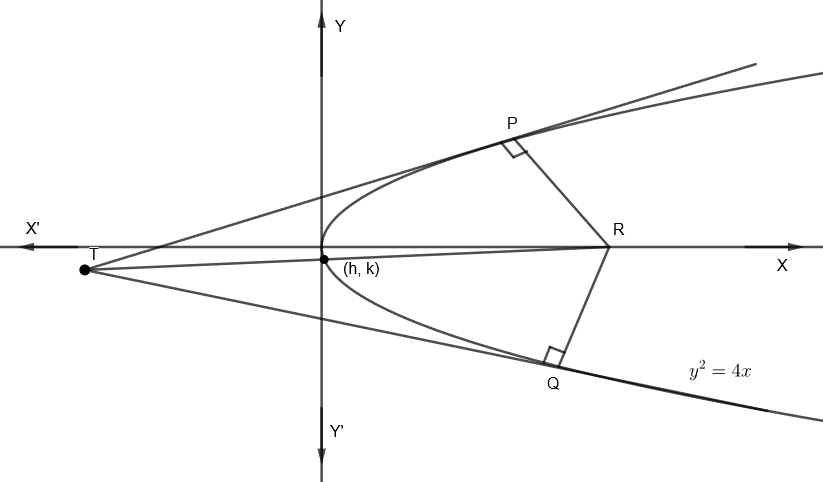
From the figure we can understand that TP and TQ are the tangents to the parabola \[{{y}^{2}}=4x\]. And the normals of P and Q meet at R where \[\angle TPR={{90}^{o}}\] and \[\angle TQR={{90}^{o}}\].

Now by joining the points T and R. Then TPR becomes a right angled triangle. So, we need to find the locus of the center of the circle circumscribing \[\Delta TPQ\].

Here in \[\Delta TPR\], the circumcenter is the midpoint of TR (i.e. hypotenuse of \[\Delta TPR\])

Let us take the coordinates of the midpoint of TR as (h, k). See the figure to find the exact place of the circumcenter.

(h, k) is the midpoint of T and R.

\[T\left( a{{t}_{1}}{{t}_{2}},a\left( {{t}_{1}}+{{t}_{2}} \right) \right)\] and \[R\left[ a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}}+2 \right),-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right) \right]\]

The formula to midpoint \[\Rightarrow \left(
\dfrac{{{x}_{2}}+{{x}_{1}}}{2},\dfrac{{{y}_{2}}+{{y}_{1}}}{2} \right)\]

\[\therefore h=\dfrac{{{x}_{2}}+{{x}_{1}}}{2}\] and \[k=\dfrac{{{y}_{2}}+{{y}_{1}}}{2}\]

\[\therefore h=\dfrac{a\left( t_{1}^{2}+t_{2}^{2}+{{t}_{1}}{{t}_{2}}+2

\right)+a{{t}_{1}}{{t}_{2}}}{2}\]

\[=\dfrac{at_{1}^{2}+at_{2}^{2}+a{{t}_{1}}{{t}_{2}}+2a+a{{t}_{1}}{{t}_{2}}}{2}\]

\[=\dfrac{a\left( t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}}+2 \right)}{2}\]

\[k=\dfrac{-a{{t}_{1}}{{t}_{2}}\left( {{t}_{1}}+{{t}_{2}} \right)+a\left( {{t}_{1}}+{{t}_{2}}
\right)}{2}\]

\[=\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)}{2}\]

\[\therefore \left( h,k \right)=\left[ \dfrac{a\left( t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}}+2
 \right)}{2},\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)}{2}
\right]....\left( iii \right)\]

Here, the given equation of parabola is \[{{y}^{2}}=4x\], where a = 1.

When the value of a = 1, by simplifying equation (iii), we get it equal to
\[{{k}^{2}}=\dfrac{h-1}{2}\].

\[k=\dfrac{a\left( {{t}_{1}}+{{t}_{2}} \right)\left( 1-{{t}_{1}}{{t}_{2}} \right)}{2}\]

The chord joining \[\left( at_{1}^{2},2a{{t}_{1}} \right)\] and \[\left( at_{2}^{2},2a{{t}_{2}} \right)\] passes through the focus, if \[{{t}_{1}}{{t}_{2}}=-1\] [i.e. the tangents are perpendicular]

Put a = 1 and \[{{t}_{1}}{{t}_{2}}=-1\]

\[k=\dfrac{\left( {{t}_{1}}+{{t}_{2}} \right)\left[ 1-\left( -1 \right) \right]}{2}=\left( {{t}_{1}}+{{t}_{2}} \right)\times \dfrac{2}{2}={{t}_{1}}+{{t}_{2}}\]

\[\therefore k={{t}_{1}}+{{t}_{2}}\]

Now, squaring both the sides, we get

\[{{k}^{2}}={{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}={{t}_{1}}+{{t}_{2}}+2{{t}_{1}}{{t}_{2}}\]

Substitute \[{{t}_{1}}{{t}_{2}}=-1\]

\[\Rightarrow {{k}^{2}}={{t}_{1}}+{{t}_{2}}+2\left( -1 \right)\]

\[\therefore {{k}^{2}}={{t}_{1}}+{{t}_{2}}-2.....\left( iv \right)\]

Now, \[h=\dfrac{a\left( t_{1}^{2}+t_{2}^{2}+2{{t}_{1}}{{t}_{2}}+2 \right)}{2}\]

Put a = 1 and \[{{t}_{1}}{{t}_{2}}=-1\]

\[\therefore h=\dfrac{t_{1}^{2}+t_{2}^{2}+2\left( -1
\right)+2}{2}=\dfrac{t_{1}^{2}+t_{2}^{2}}{2}\]

\[h-1\Rightarrow \dfrac{t_{1}^{2}+t_{2}^{2}}{2}-1\]

\[h-1\Rightarrow \dfrac{t_{1}^{2}+t_{2}^{2}-2}{2}\]

\[\therefore \dfrac{h-1}{2}\Rightarrow t_{1}^{2}+t_{2}^{2}-2....\left( v \right)\]

By comparing equations (iv) and (v), we can come to the conclusion that

\[{{k}^{2}}=\dfrac{h-1}{2}\]

Putting (x, y) in place of (h, k), we get

\[{{y}^{2}}=\dfrac{x-1}{2}....\left( vi \right)\]

Now, considering equation (vi), it’s the equation of a parabola,

\[{{y}^{2}}=\dfrac{1}{2}\left( x-1 \right)\]

where the vertex is (1, 0)

It’s obtained by putting y = 0.

\[0=\dfrac{1}{2}\left( x-1 \right)\]

\[\Rightarrow x=1\]

Therefore, vertex is (1, 0) and the value of \[4a=\dfrac{1}{2}\].

\[\Rightarrow a=\dfrac{1}{2\times 4}=\dfrac{1}{8}\]

Therefore, the focus is obtained by (1+a, 0).

\[F\left( 1+\dfrac{1}{8},0 \right)=F\left( \dfrac{9}{8},0 \right)\]

To find the foot of the directrix \[{{F}_{D}}\], the directrix will come behind the parabola, which is at a distance of (1 – a) from the parabola.

Here, the y – coordinate is zero, as the components lie in the x – axis.

Therefore, foot of directrix = (1 – a, 0)

\[{{F}_{D}}=\left( 1-\dfrac{1}{8},0 \right)=\left( \dfrac{7}{8},0 \right)\]

We know that the length of latus rectum = 4a

\[=4\times \dfrac{1}{8}=\dfrac{1}{2}\]

Therefore, we got the values of the parabola, where the locus of the center of the circle circumscribes the triangle \[\Delta TPQ\].

\[\begin{align}

  & \text{Vertex}=\left( 1,0 \right) \\

 & \text{Focus}=\left( \dfrac{9}{8},0 \right) \\

 & \text{Foot of Directrix}=\left( \dfrac{7}{8},0 \right) \\

 & \text{Length of latus rectum}=\dfrac{1}{2} \\

\end{align}\]

Hence the correct options are (a), (b) and (d).

Note: By taking the value of a = 1, as per the equation of parabola \[{{y}^{2}}=4x\], we obtain the simplified form of (h, k) as \[{{k}^{2}}=h-\dfrac{1}{2}\]. From this, we get the values of vertex, focus, foot of directrix and length of latus rectum.