Question

How many triangles are there in the following figure?

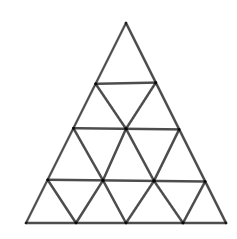
(a)19
(b)21
(c)27
(d)48

Answer 1

Hint: Consider 4 levels of the triangles. Count the small triangles from each 4 levels. Now manage each levels like \[\left( 1+2 \right),\left( 2+3 \right),\left( 3+4 \right),\left( 1+2+3 \right),\left( 2+3+4 \right)\] and \[\left( 1+2+3+4 \right)\] levels and get the no. of triangles. Add all three together to get a total no. of triangles.

Complete step-by-step answer:

Consider the figure given to us. We need to find the no. of triangles from the figure. Let us name the triangle. So, it becomes easy for us to identify the triangles.

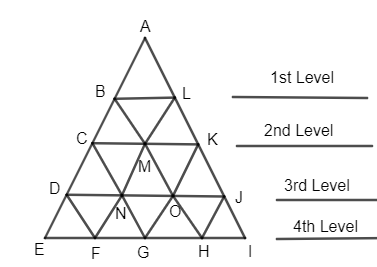
Let us consider the figure which we have named.
At first level, we have an ABL triangle.
\[\therefore \] At 1st level there is 1 triangle.
Now at the second level we have the triangle, BCM, BLM and LMK.
Thus, there are 3 triangles at second level.
Now in the 3rd level, we have the triangles CDN, CMN, MNO, MOK and KOJ.
Thus, there are 5 triangles in the 3rd level.
In the 4th level, we have the triangle DEF, DFN, NFG, GNO, OGH, HOJ and JHI.
i.e., there are 7 triangles on 4th level.
\[\therefore \] No. of triangle in all 4 levels \[=\] 1st level + 2nd level + 3rd level + 4th level
\[=1+3+5+7=16\]
\[\therefore \] No, of small triangles in the given figure \[=\] 16 …………………………….(1)
Now let us merge different levels.
Let us merge (1st + 2nd) level. We get \[\Delta ACK\] i.e. 1 triangle.
Merging (2nd + 3rd) level, we get triangles BDO and LNJ i.e. 2 triangles.
Merging (3rd + 4th) level, we get triangles CEG, CGK, KGJ and CGK i.e. 4 triangles.
Merging (1st + 2nd + 3rd) level, we get triangles ADJ i.e. 1 triangle.
By merging (2nd + 3rd + 4th) level, we get triangles BEH and LFJ i.e. 2 triangles.
Now merging all levels, we get the \[\Delta AEJ\] i.e. 1 triangle.
Thus, the no. of triangle we obtained by merging \[=\] No. of triangle by (1st + 2nd) level + (2nd + 3rd) level + (3rd + 4th) level + (1st + 2nd + 3rd) level + (2nd + 3rd + 4th) level + (1st + 2nd + 3rd + 4th) level
\[=1+2+4+1+2+1=11\]
\[\therefore \] No. of triangle by merging levels \[=11\] ……………………………….(2)
Now add (1) and (2) to get the total no. of triangles.
\[\therefore \] Total no. of triangles \[=\] No. of small triangles + No. of triangle by levels
$=16+11=27$
\[\therefore \] Total number of triangles \[=\] 27.
\[\therefore \] Option (c) is the correct answer.

Note: If you miss counting at least one triangle that can be formed, thus you will get the wrong answer. You can also count it without all these steps, but it will get you wrong at one place. Thus, write down steps to get the correct answer.