Question

Two adjacent angles of a parallelogram are in ratio 1: 5. Find all the angles of the parallelogram.

Answer 1

Hint: In this question we have to find the value of angles of parallelogram and ratio of 2 angles is given. We know that the opposite angles of the parallelogram are equal, and the total sum of all the angles of the parallelogram is equal to $360^\circ $ . So, we will let the two adjacent angles of the parallelogram be $1x$ and $5x$ . And then we will find the value of $x$ using the mentioned properties of a parallelogram.

Complete step-by-step solution:
It is given that the ratio of the two adjacent angles of the parallelogram is1: 5. Let us consider the common factor of the ratio of the two adjacent angles of the parallelogram by $x$. Thus, the two adjacent angles of the parallelogram will become $x$ and $5x$ .

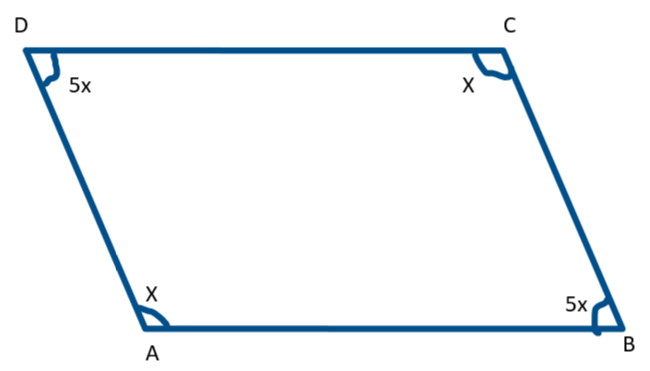
It is known that the opposite angles of the parallelogram are equal. Therefore, the other two angles of the parallelogram must be equal to the $x$ and $5x$ . Thus, the four angles of the parallelogram become $x$ , $5x$ , $x$ , $5x$ . We also know that the total sum of the interior angles of any polygon with four sides is $360^\circ $ .
Thus, the sum of $x$ , $5x$ , $x$ , $5x$ is equal to $360^\circ $ .
$x + 5x + x + 5x = 360^\circ $
$\Rightarrow 12x = 360^\circ $
$\Rightarrow x = \dfrac{{360^\circ }}{{12}}$
$\Rightarrow x = 30^\circ $
So, 2 angles will be $30^\circ $ each.
Now, we will find other 2 angles.
$\Rightarrow 5x = 30^\circ \times 5$
$\Rightarrow 5x = 150^\circ $
The other 2 angles are $150^\circ $ each.
Hence, the angles of parallelogram are $30^\circ $ , $50^\circ $ , $30^\circ $ and $50^\circ $.

Note: We know that the sum of angles of parallelogram is \[{360^ \circ }\] . And if in the question adjacent angles are to be found then, we will use the property that the sum of adjacent angles of parallelogram is \[{180^ \circ }\] . Here we should know the properties of a parallelogram or other quadrilaterals.