Question

Two adjacent angles of a parallelogram have equal measure. Find the measure of each of the angles of the parallelogram.

Answer 1

Hint – Let ABCD be a parallelogram with $\angle A = \angle B$. Use the concept that the sum of adjacent angles is equal to 180 degrees.

Complete step-by-step solution -
Refer to the figure below of parallelogram ABCD-

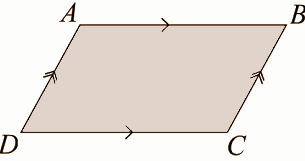
We have been given in the question that adjacent angles of a parallelogram are equal.
To find: Measure of each angle of the parallelogram.
Let ABCD be a parallelogram with $\angle A = \angle B$.
Now, we know that: Sum of adjacent angles $ = {180^ \circ }$.
$\angle A + \angle B = {180^ \circ }$
Putting $\angle A = \angle B$ in the above equation, we get-
$
  \angle A + \angle A = {180^ \circ } \\
   \Rightarrow 2\angle A = {180^ \circ } \\
   \Rightarrow \angle A = \angle B = {90^ \circ } \\
 $
Now, we know the opposite angles of a parallelogram are equal.
Therefore, $\angle C = \angle A = {90^ \circ }$(Opposite angles)
And also, $\angle D = \angle B = {90^ \circ }$(Opposite angles)
Thus, each angle of the parallelogram measures ${90^ \circ }$.
Thus, the parallelogram with each angle 90 degrees is shown below-

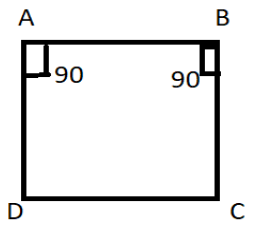
Note – Whenever such types of question appear, assume a parallelogram and then use the conditions given in the question. As mentioned in the solution, the adjacent angles are equal, i.e., $\angle A = \angle B$, so using the concept that the sum of adjacent angles is equal to 180 degrees, find the angles A and B, and then C and D angles can be found out by the property that opposite angles of parallelogram are equal.