Two adjacent sides of a parallelogram are \[2\hat{i}-4\hat{j}+5\hat{k}\] and \[\hat{i}-2\hat{j}-3\hat{k}\]. Find the unit vectors parallel to both the diagonals. Also, find the area of the parallelogram.
Answer
Verified358.5k+ views
Hint: Diagonal vectors of a parallelogram are the sum and difference of the adjacent side vectors. Area vector of a parallelogram is just the cross product between two adjacent sides.
Complete step-by-step answer:
Let \[\vec{A}=2\hat{i}-4\hat{j}+5\hat{k}\] and \[\vec{B}=\hat{i}-2\hat{j}-3\hat{k}\]
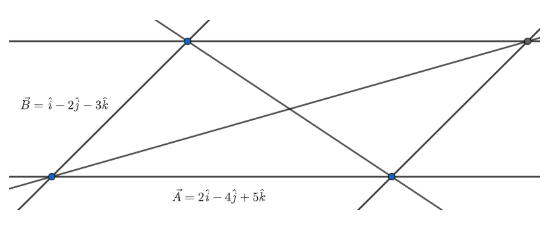
We know that if two adjacent vectors make a parallelogram then the principal diagonal vector is the sum of the two vectors and the other diagonal is the difference between two vectors. This is because of the triangle rule of addition of vectors.
The principal diagonal vector is, \[\vec{P}\] = \[\vec{A}+\vec{B}=(2\hat{i}-4\hat{j}+5\hat{k})+(\hat{i}-2\hat{j}-3\hat{k})=3\hat{i}-6\hat{j}+2\hat{k}\]
And the other diagonal vector is, \[\vec{Q}\] = \[\vec{A}-\vec{B}=(2\hat{i}-4\hat{j}+5\hat{k})-(\hat{i}-2\hat{j}-3\hat{k})=\hat{i}-2\hat{j}+8\hat{k}\]
We know that unit vector parallel to any vector\[\vec{R}\] is \[\dfrac{{\vec{R}}}{\left| {\vec{R}} \right|}\].
Hence, Unit vector parallel to \[\vec{P}\] = \[\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\left| 3\hat{i}-6\hat{j}+2\hat{k} \right|}=\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\sqrt{{{3}^{2}}+{{(-6)}^{2}}+{{2}^{2}}}}=\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\sqrt{49}}=\dfrac{3}{7}\hat{i}-\dfrac{6}{7}2\hat{j}+\dfrac{2}{7}\hat{k}\] and unit vector parallel to \[\vec{Q}\] = \[\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\hat{i}-2\hat{j}+8\hat{k}}=\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\sqrt{{{1}^{2}}+{{(-2)}^{2}}+{{8}^{2}}}}=\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\sqrt{69}}=\dfrac{1}{\sqrt{69}}\hat{i}-\dfrac{2}{\sqrt{69}}2\hat{j}+\dfrac{8}{\sqrt{69}}\hat{k}\]
Now, we know that the area vector of a parallelogram bounded by two adjacent side vectors is the cross product between them.
Therefore, area of the parallelogram is \[\vec{A}\times \vec{B}=\left( \begin{matrix}
{\hat{i}} & {\hat{j}} & {\hat{k}} \\
2 & -4 & 5 \\
1 & -2 & -3 \\
\end{matrix} \right)=\hat{i}[(-4)(-3)-5(-2)]-\hat{j}[(2(-3)-(5)(1)]+\hat{k}[2(-2)-1(-4)]=22\hat{i}+11\hat{j}\]
Hence, the value of the area of the parallelogram is \[\left| \vec{A}\times \vec{B} \right|=\sqrt{{{22}^{2}}+{{11}^{2}}}=\sqrt{484+121}=\sqrt{505}\] units.
Note: Unit vector parallel to a vector means unit vector of that vector in that direction. Keep in mind while finding the area using cross product. The area vector may be negative but the modulus value will be positive only.
Complete step-by-step answer:
Let \[\vec{A}=2\hat{i}-4\hat{j}+5\hat{k}\] and \[\vec{B}=\hat{i}-2\hat{j}-3\hat{k}\]
We know that if two adjacent vectors make a parallelogram then the principal diagonal vector is the sum of the two vectors and the other diagonal is the difference between two vectors. This is because of the triangle rule of addition of vectors.
The principal diagonal vector is, \[\vec{P}\] = \[\vec{A}+\vec{B}=(2\hat{i}-4\hat{j}+5\hat{k})+(\hat{i}-2\hat{j}-3\hat{k})=3\hat{i}-6\hat{j}+2\hat{k}\]
And the other diagonal vector is, \[\vec{Q}\] = \[\vec{A}-\vec{B}=(2\hat{i}-4\hat{j}+5\hat{k})-(\hat{i}-2\hat{j}-3\hat{k})=\hat{i}-2\hat{j}+8\hat{k}\]
We know that unit vector parallel to any vector\[\vec{R}\] is \[\dfrac{{\vec{R}}}{\left| {\vec{R}} \right|}\].
Hence, Unit vector parallel to \[\vec{P}\] = \[\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\left| 3\hat{i}-6\hat{j}+2\hat{k} \right|}=\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\sqrt{{{3}^{2}}+{{(-6)}^{2}}+{{2}^{2}}}}=\dfrac{3\hat{i}-6\hat{j}+2\hat{k}}{\sqrt{49}}=\dfrac{3}{7}\hat{i}-\dfrac{6}{7}2\hat{j}+\dfrac{2}{7}\hat{k}\] and unit vector parallel to \[\vec{Q}\] = \[\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\hat{i}-2\hat{j}+8\hat{k}}=\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\sqrt{{{1}^{2}}+{{(-2)}^{2}}+{{8}^{2}}}}=\dfrac{\hat{i}-2\hat{j}+8\hat{k}}{\sqrt{69}}=\dfrac{1}{\sqrt{69}}\hat{i}-\dfrac{2}{\sqrt{69}}2\hat{j}+\dfrac{8}{\sqrt{69}}\hat{k}\]
Now, we know that the area vector of a parallelogram bounded by two adjacent side vectors is the cross product between them.
Therefore, area of the parallelogram is \[\vec{A}\times \vec{B}=\left( \begin{matrix}
{\hat{i}} & {\hat{j}} & {\hat{k}} \\
2 & -4 & 5 \\
1 & -2 & -3 \\
\end{matrix} \right)=\hat{i}[(-4)(-3)-5(-2)]-\hat{j}[(2(-3)-(5)(1)]+\hat{k}[2(-2)-1(-4)]=22\hat{i}+11\hat{j}\]
Hence, the value of the area of the parallelogram is \[\left| \vec{A}\times \vec{B} \right|=\sqrt{{{22}^{2}}+{{11}^{2}}}=\sqrt{484+121}=\sqrt{505}\] units.
Note: Unit vector parallel to a vector means unit vector of that vector in that direction. Keep in mind while finding the area using cross product. The area vector may be negative but the modulus value will be positive only.
Last updated date: 17th Sep 2023
•
Total views: 358.5k
•
Views today: 3.58k
