Question

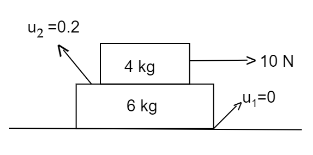
Two blocks of mass \[4{\text{ kg}}\] and \[{\text{6 kg}}\]are placed one over the other. If a force of \[{\text{10 N}}\] is applied on the block of mass \[4{\text{ kg}}\], then the acceleration of the two blocks at the instant shown is \[\left( {{\text{g = 10 m/}}{{\text{s}}^2}} \right)\]

Answer 1

Hint:To solve this question, assume both the block are moving together with a common acceleration. Find the common acceleration and the minimum friction force required for both the block to move together. Compare if the force required is less than or equal to the limiting frictional force. If yes, our assumption is correct and both the blocks move with the common acceleration else kinetic friction is acting, draw the free-body diagrams of each block and find the acceleration of the blocks, respectively.

Formula used:
\[F = ma\]
Where \[F\] is the total force, \[m\] is the mass of the system and \[a\] is the net acceleration of the system.
\[f = \mu N\]
Where \[f\] is the limiting frictional force, \[\mu \] is the coefficient of friction and \[N\] is the normal force acting.

Complete step by step answer:
We are given, a Force of \[{\text{10 N}}\] is applied on \[4{\text{ kg}}\] block and the friction coefficient between the blocks is \[{\mu _2} = 0.2\] and ground is smooth. Let us assume both the blocks are moving together with a common acceleration of \[a{\text{ }}m/{s^2}\].Total mass of the system is \[10{\text{ }}kg\]. As friction becomes an internal force for the system of the block Net force acting on the system is \[{\text{F = 10 N}}\].
\[F = ma\]
\[ \Rightarrow 10 = 10a\]
\[ \Rightarrow a = 1{\text{ m/}}{{\text{s}}^2}\]

Now, let's find out the minimum frictional force required so that the blocks move with common acceleration.
For \[4{\text{ kg}}\] block,
\[N = mg = 4g\]
\[{f_{\max }} = \mu \times 4g\]
\[ \Rightarrow {f_{\max }} = 0.2 \times 4 \times 10 = 8{\text{ N}}\]

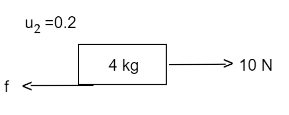
Net force acting on \[4{\text{ kg}}\] block is \[{\text{10 - f}}\]
\[ \Rightarrow {\text{10 - f = 4a}}\]
\[ \Rightarrow {\text{10 - f = 4}} \times {\text{1}}\]
\[ \Rightarrow {\text{f}} = 6{\text{ N}}\]
From this we can conclude that the required friction is less than the limiting friction
\[{\text{f}} \leqslant {f_{\max }}\]

Therefore, our assumption was correct that both the blocks move with the common acceleration of \[1{\text{ m/}}{{\text{s}}^2}\].

Note:If the required friction value would have been greater than the limiting friction then both the blocks would have different accelerations. To find out the acceleration of each block we need to write the force-mass equation \[\left( {F = ma} \right)\] on both the blocks. Limiting friction would have been acting on both the blocks and they would be slipping over each other.