Question

Two bodies, each of mass M, are fixed at a separation 2L. A particle of mass m is projected from the midpoint of the line joining their centres, perpendicular to the line. The gravitational constant is G. Then the correct statement is
\[\begin{align}
  & \text{A) The minimum initial velocity of the mass m to escape the gravitational field of the two bodies is 4}\sqrt{\dfrac{GM}{L}} \\
 & \text{B) The minimum initial velocity of the mass m to escape the gravitational field of the two bodies is 2}\sqrt{\dfrac{GM}{L}} \\
 & \text{C) The minimum initial velocity of the mass m to escape the gravitational field of the two bodies is }\sqrt{\dfrac{2GM}{L}} \\
 & \text{D) The energy of the mass m remains constant}\text{.} \\
\end{align}\]

Answer 1

Hint: Here we have to find the correct statement from the given option when a particle of mass m is projected from the midpoint of the line joining centres of other two objects of equal masses. We have to find the escape velocity for the particle of mass m. So we will find the escape velocity by using the law of conservation of energy.
Formula used:
\[\begin{align}
  & K.E.=\dfrac{1}{2}m{{v}^{2}} \\
 & P.E.=-\dfrac{GMm}{L} \\
\end{align}\]

Complete answer:
First let us draw a diagram for better understanding of the question.

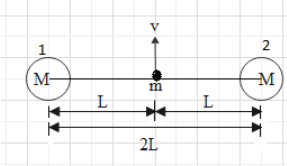
So here m is the mass which is projected from the midpoint of line of length 2L which is joining the centres bodies of masses M. As it is placed at midpoint of the line therefore distance from each mass is L. Let v be the escape velocity. When the particle is escaped from the gravitational pull experienced by the objects of masses M. When it escapes its kinetic energy and the potential energy becomes zero.
Then according to law of conservation of energy we can write
\[K.E.+P.E{{.}_{1}}+P.E{{.}_{2}}\text{=0 }.........\text{(i)}\]
Where K.E. is the kinetic energy of the mass m and \[P.E{{.}_{1}}\]is the potential energy due to object 1 and \[P.E{{.}_{2}}\]is the potential energy due to object 2. Now the formula of K.E. and P.E. are
\[\begin{align}
  & K.E.=\dfrac{1}{2}m{{v}^{2}} \\
 & P.E.=-\dfrac{GMm}{L} \\
\end{align}\]
Hence we can rewrite the equation (i) as
\[\begin{align}
  & \dfrac{1}{2}m{{v}^{2}}+\left( -\dfrac{GMm}{L} \right)+\left( -\dfrac{GMm}{L} \right)=0 \\
 & \Rightarrow \dfrac{1}{2}m{{v}^{2}}-\dfrac{GMm}{L}-\dfrac{GMm}{L}=0 \\
 & \Rightarrow \dfrac{1}{2}m{{v}^{2}}=\dfrac{GMm}{L}+\dfrac{GMm}{L} \\
 & \Rightarrow \dfrac{1}{2}m{{v}^{2}}=\dfrac{2GMm}{L} \\
 & \Rightarrow {{v}^{2}}=\dfrac{4GMm}{mL} \\
 & \Rightarrow {{v}^{2}}=\dfrac{4GM}{L} \\
 & \Rightarrow v=\sqrt{\dfrac{4GM}{L}} \\
 & \Rightarrow v=2\sqrt{\dfrac{GM}{L}} \\
\end{align}\]

Hence, option B is the correct answer.

Note:
Here the potential energy experienced due to object 1 and 2 are the same because their masses are the same. And the distance of the mass m from both the objects are the same. The energy of the mass doesn’t remain constant because when an object is escaped its kinetic and potential energy or gravitational potential energy is zero.