Question

Two cars are moving in the same direction with a speed of 30km/hr. They are separated from each other by 5km. Third car moving in the opposite direction meets the two cars after an interval of 4 minutes. What is the speed of the third car?
A. 35km/hr
B. 40km/hr
C .45km/hr
D. 75km/hr

Answer 1

Hint: View the scenario taking the second car as the reference frame. Apply distance formula on car3 to find its velocity. Use the formula for relative velocity which is \[\overrightarrow{{{V}_{AB}}}=\overrightarrow{{{V}_{A}}}-\overrightarrow{{{V}_{B}}}\] and the formula for speed, $\text{speed}=\dfrac{\text{distance}}{\text{time}}$.

Complete step by step answer:
Let the velocity of the first two cars be ${{v}_{1}}=30km/hr$ and ${{v}_{2}}=30km/hr$, the distance between them be $d=5km$.
Since the velocities of the two cars are the same, the relative speed between them is zero. That is, for a person in car2, car1 seems stationary. This also implies that the distance between car1 and car2 is $d=5km$throughout the motion.
Let us assume that car3 has a velocity $-xkm/hr$ since it is moving in the opposite direction as of car1 and car2.
We take car2 as the reference frame. From this frame, it seems that on a 1-dimension plane, two points (car1 and car2) are separated by a distance $d$. And car3 is approaching the points.

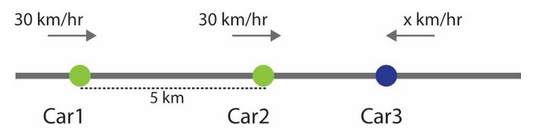
The velocity of car3 observed by a person in car2 will be:
\[\overrightarrow{{{V}_{32}}}=\overrightarrow{{{V}_{3}}}-\overrightarrow{{{V}_{2}}}=-x-30=-\left( x+30 \right)km/hr\]
It is given that the time taken by car3 to cross the other cars is
$t=4\text{min}=\dfrac{4}{60}hr=\dfrac{1}{15}hr$ .
Since, we are dealing with a 1-dimensional problem, let us only take speed and distance into consideration.
Applying the basic formula for speed,
$\begin{align}
  & \text{speed}=\dfrac{\text{distance}}{\text{time}} \\
 & \Rightarrow 30+x=\dfrac{5}{1/15}=75km/hr \\
 & \Rightarrow x=45km/hr \\
\end{align}$
Therefore, option C. is the correct answer.

Note: Since, car1 and car2 had the same velocities, taking any one car as the reference frame did the job. But, be careful while applying this concept to other questions. Car1 and car2 might move with respect to one another.