Question

Two circles of radii 5cm and 3cm intersect at two points and the distance between their centers is 4 cm. Find the length of the common chord.

Answer 1

Hint: Let the common chord AB in two circles having P and Q as the center. AP is the radius of the first circle having length 5cm and AQ is the radius of the other circle having length 3cm. Now, segment PQ is perpendicular to the chord AB using the theorem “The perpendicular from center to the chord, bisect the chord”. Therefore, the length of AR is the half of the length AB using the theorem. After that using Pythagoras Theorem in the both triangle ARP and triangle ARQ. We get the value of length of AR, so the length of AB is half of the length of AR.

Complete step-by-step answer:
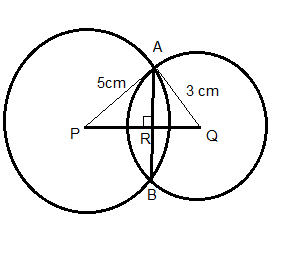
Let the common chord be AB. P and Q are the centers of circles.
The length of AP is given in the question, \[AP=5cm\].
The length of PQ is also given in the question, \[PQ=4cm\].
Using the theorem “The perpendicular from center to the chord, bisect the chord”.
Hence, the segment PQ is perpendicular to the chord AB.
$\therefore AR=RB=\dfrac{1}{2}AB$
Let the length of PR be x cm.
So, the length of RQ $=(4-x)cm$.
Now, consider the triangle ARP and apply Pythagoras Theorem in it:
In triangle ARP,
$\begin{align}
  & A{{P}^{2}}=A{{R}^{2}}+P{{R}^{2}} \\
 & A{{R}^{2}}={{\left( 5 \right)}^{2}}-{{x}^{2}} \\
 & A{{R}^{2}}=25-{{x}^{2}}...(1) \\
\end{align}$
Applying the Pythagoras Theorem in the triangle ARQ,
$\begin{align}
  & A{{Q}^{2}}=A{{R}^{2}}+Q{{R}^{2}} \\
 & A{{R}^{2}}={{\left( 3 \right)}^{2}}-{{\left( 4-x \right)}^{2}}....(2) \\
\end{align}$
Using equation (1) and equation (2), we get:
$\begin{align}
  & \therefore {{5}^{2}}-{{x}^{2}}={{3}^{2}}-{{\left( 4-x \right)}^{2}} \\
 & 25-{{x}^{2}}=9-(16-8x+{{x}^{2}}) \\
\end{align}$
We expand the ${{(4-x)}^{2}}$ using the identity ${{(a-b)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab$ .
Solving further,
$\begin{align}
  & 25-{{x}^{2}}=-7+8x-{{x}^{2}} \\
 & 32=8x \\
 & \therefore x=4 \\
\end{align}$
Putting the value of x, in equation number 1, we get:
$\begin{align}
  & A{{R}^{2}}=25-16 \\
 & \therefore AR=3cm \\
 & \therefore AB=2\times AR=2\times 3 \\
 & \therefore AR=6cm. \\
\end{align}$
Hence, the length of the common chord AB is 6cm.

Note: The key step for solving this problem is the stated theorem for chord. After using that theorem and further applying the Pythagoras principle we got the solution to our problem. The definition of the common chord of two circles is also very important without which the visualisation of the problem would have been difficult.