Question

Two circles touch externally. The sum of their areas is $130\pi $sq. cm and the distance between their centres is 14cm. Find the radii of the circles.
A. 11cm & 3cm
B. 1cm & 3cm
C. 11cm & 13cm
D. None of these

Answer 1

Hint: Consider 2 triangles with centre ${{r}_{1}}$and${{r}_{2}}$. We have been given combined area and distance between centres of radius. Substitute there in the sum of areas. Simplify it to a quadratic equation and roots will give the radius of both circles.

Complete step-by-step answer:
Let us consider two circles with centres ${{O}_{1}}$ and ${{O}_{2}}$. Let ${{r}_{1}}$be the radius of circle 1 and ${{r}_{2}}$ be the radius of circle 2.

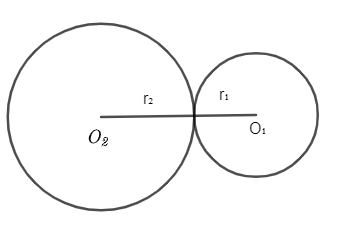
Given that the distance between the centers of circle 1 and 2 is 14cm.

$\begin{align}
& \Rightarrow {{r}_{1}}+{{r}_{2}}=14 \\
& \therefore {{r}_{2}}=14-{{r}_{1}}\ldots \ldots (1) \\
\end{align}$

Given that the sum of areas of 2 circles is $130\pi $

Let ${{A}_{1}}$ be the area of circle 1 and ${{A}_{2}}$be the area of circle 2.

$\therefore {{A}_{1}}+{{A}_{2}}=130\pi \ldots \ldots (2)$

We know area, \[A=\pi {{r}^{2}}\]

$\therefore {{A}_{1}}=\pi {{r}_{1}}^{2},{{A}_{2}}=\pi {{r}_{2}}^{2}$; cancel $\pi $ from RHS & LHS
$\therefore \pi {{r}_{1}}^{2}+\pi {{r}_{2}}^{2}=130\ldots \ldots (3)$
Substitute equation (1) in equation (3)
${{r}_{1}}^{2}+{{\left( 14-{{r}_{1}} \right)}^{2}}=130$
We know that,
$\begin{align}
& {{\left( a-b \right)}^{2}}={{a}^{2}}-2ab+{{b}^{2}} \\
& \Rightarrow {{r}_{1}}^{2}+{{14}^{2}}-2\times 14{{r}_{1}}+{{r}_{1}}^{2}=130 \\
& \Rightarrow {{r}_{1}}^{2}-28{{r}_{1}}+{{r}_{1}}^{2}=130-96 \\
& \therefore 2{{r}_{1}}^{2}-28{{r}_{1}}=-66 \\
& \Rightarrow 2{{r}_{1}}^{2}-28{{r}_{1}}+66=0\ldots \ldots (4) \\
\end{align}$
Divide throughout by 2 in equation (4)
$\Rightarrow {{r}_{1}}^{2}-14{{r}_{1}}+33=0\ldots \ldots (5)$

The obtained equation (5) is similar to the general equation $a{{x}^{2}}+bx+c=0$. So comparing them we get a=1, b=-14, c=33.
Substitute the values in quadratic equation,
$\begin{align}
& \dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}=\dfrac{-(-14)\pm \sqrt{{{\left( -14 \right)}^{2}}-4\times 1\times 33}}{2\times 1} \\
& =\dfrac{14\pm \sqrt{196-32}}{2}=\dfrac{14\pm \sqrt{64}}{2}=\dfrac{14\pm 8}{2} \\
\end{align}$
$\therefore $Roots are $\left( \dfrac{14+8}{2} \right)$and $\left( \dfrac{14-8}{2} \right)$= 11 and 3 cm.
$\therefore $${{r}_{1}}$=11cm
${{r}_{2}}$=14-${{r}_{1}}$=3cm

Radii of two circles are 11cm and 3cm.

Note: When ${{r}_{1}}$=11cm, substituting ${{r}_{2}}$=14-11=3cm. Similarly if ${{r}_{1}}$=3cm, substituting ${{r}_{2}}$=14-3=11cm
So the radius of two circles is 11cm and 3cm, irrespective of where the bigger and smaller circle comes.