Question

Two circles touch internally. The sum of their area is \[116\pi c{{m}^{2}}\] and the distance between their centers is 6cm. Find the radii of the circles.

Answer 1

Hint: Draw a diagram of the given situation. Assume the radius of the bigger circle as R and the radius of the smaller circle as r. Take the difference of their radius and equate it with 6 to form an equation. Now, apply the formula for area of circle given as: - Area = \[\pi \times {{\left( radius \right)}^{2}}\] and take the sum of their areas and equate it with \[116\pi \] to form another equation. Solve the two equations formed to get the value of R and r.

Complete step-by-step solution
We have been given that two circles are touching internally. Let us draw a diagram of the given condition.

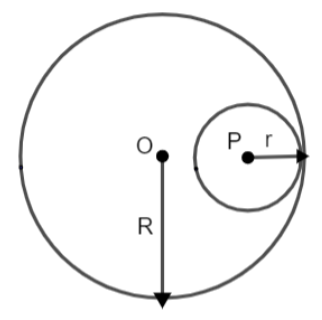
In the above figure, we have assumed two circles with center O and P. the bigger circle is having radius R and the smaller circle is having radius r. Now, let us come to the information given in the question.
In the first condition, it is given that the distance between the centers of the circle is 6cm.
We know that the distance between the centres of two circles touching internally is the difference between their radius. Therefore, mathematically, we have,
\[\Rightarrow R-r=6\] - (1)
Now, the second condition is given that the sum of their area is \[116\pi c{{m}^{2}}\]. So, applying the formula for the area of a circle given as: - Area = \[\pi \times {{\left( radius \right)}^{2}}\], we get,
A = Area of bigger circle = \[\pi {{R}^{2}}\]
Similarly, we have,
a = area of smaller circle = \[\pi {{r}^{2}}\]
Now, taking the sum of areas of the two circles, we get,
\[\begin{align}
  & \Rightarrow \pi {{R}^{2}}+\pi {{r}^{2}}=116\pi \\
 & \Rightarrow \pi \left( {{R}^{2}}+{{r}^{2}} \right)=116\pi \\
\end{align}\]
Cancelling ‘\[\pi \]’ from both sides, we get,
\[\Rightarrow {{R}^{2}}+{{r}^{2}}=116\] - (2)
Squaring equation (1) and using the identity, \[\Rightarrow {{\left( a-b \right)}^{2}}={{a}^{2}}+{{b}^{2}}-2ab\], we get,
\[\begin{align}
  & \Rightarrow {{\left( R-r \right)}^{2}}={{6}^{2}} \\
 & \Rightarrow {{R}^{2}}+{{r}^{2}}-2rR=36 \\
\end{align}\]
Substituting the value of \[{{R}^{2}}+{{r}^{2}}\], from equation (2), we get,
\[\begin{align}
  & \Rightarrow 116-2Rr=36 \\
 & \Rightarrow 2Rr=116-36 \\
 & \Rightarrow 2Rr=80 \\
 & \Rightarrow Rr=40 \\
\end{align}\]
Now, substituting the value of R from equation (1) in the above relation, we get,
\[\begin{align}
  & \Rightarrow \left( r+6 \right)r=40 \\
 & \Rightarrow {{r}^{2}}+6r-40=0 \\
\end{align}\]
Using middle term split method, we get,
\[\begin{align}
  & \Rightarrow {{r}^{2}}+10r-4r-40=0 \\
 & \Rightarrow r\left( r+10 \right)-4\left( r+10 \right)=0 \\
 & \Rightarrow \left( r-4 \right)\left( r+10 \right)=0 \\
\end{align}\]
\[\Rightarrow r=4\] or \[-10\]
Since, radius cannot be negative, therefore x = -10, is neglected.
\[\Rightarrow r=4\]cm
Substituting r = 4 in equation (1), we get,
\[\begin{align}
  & \Rightarrow R-4=6 \\
 & \Rightarrow R=10cm \\
\end{align}\]
Hence, the radius of the bigger circle is 10cm and the radius of the smaller circle is 4cm.

Note: One may note that it is necessary for us to draw the diagram of the given situation otherwise we can get confused while solving the first part of the question. Not that while solving for the second condition we have canceled ‘\[\pi \]’ from both sides of the equation. This is done to make our calculation easy. So, we must try to cancel such constants whenever or wherever possible.