Question

Two cones with the same base radius \[8\,cm\] and height \[15\,cm\] are joined together along their bases. Find the surface area of the shape so formed.(answer to the nearest whole number)

Answer 1

Hint: This is a word problem, on reading the question first we write the data. Then we draw a diagram by combining two cones. Here we have to find the surface area of both cones. So on considering twice the surface area of the cone and then by using simple arithmetic operations we determine the solution.

Complete step by step answer:
The question is a word problem. So we read the sentences and analyse the data which is present in the given question.
Here in this question we are combining the both cones and then we are finding the surface area covered by the plane figure.

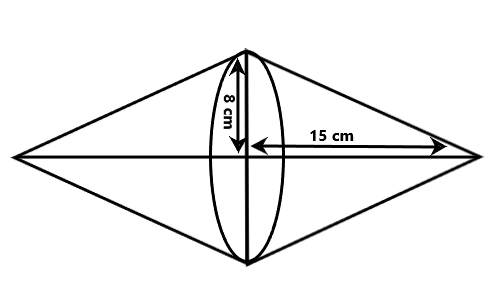
On considering the given question
The radius of a cone = \[r = 8\,cm\]
The height of a cone = \[h = 15\,cm\]
By knowing the value of radius and height of a cone we can determine the value of the slant height of cone
\[ \Rightarrow l = \sqrt {{r^2} + {h^2}} \]
On substituting the values we get
\[ \Rightarrow l = \sqrt {{8^2} + {{15}^2}} \]
On simplifying we get
\[ \Rightarrow l = \sqrt {64 + 225} \]
On adding 64 and 225
\[ \Rightarrow l = \sqrt {289} \]
On taking out square root we get
\[ \Rightarrow l = 17\,cm\]
The height can’t be negative.
Now we will determine the surface area formed by the two cones.
It is given as the sum of curved surface area of each cone.
The curved surface area of a cone is given by \[S = \pi rl\]
Now for the surface area for the shape which as formed by combining two cones is given as
\[ \Rightarrow S = 2\pi rl\]
On substituting the values to above formula we get
\[ \Rightarrow S = 2 \times \dfrac{{22}}{7} \times 8 \times 17\]
\[ \Rightarrow S = \dfrac{{2 \times 22 \times 8 \times 17}}{7}\]
On multiplying the terms
\[ \Rightarrow S = \dfrac{{5984}}{7}\]
On dividing by 7 we get
\[ \Rightarrow S = 854.85\,c{m^2}\]
On rounding off we get
\[ \Rightarrow S = 855\,c{m^2}\]

Note:
Students should be aware of the difference between TSA(Total surface area) and CSA(Curved surface area) of cone. In a mensuration problem we have to remember to write a unit. For the perimeter the unit will be the same as the unit of the given length and for the area the unit will be square units. Students must remember the units and they have to mention it.