Question

Two cubes each of volume $64c{m^2}$ are joined end to end. Find the surface area of the resulting cuboid.

Answer 1

Hint – In this question use the formula of volume of the cube which is ${(side)^3}$ to get the side of the cube. The length of the resulting cuboid is simply twice the side of the cube, the height is equal to the side of the cube and the breadth is also equal to the side of the cube.

Complete step-by-step answer:

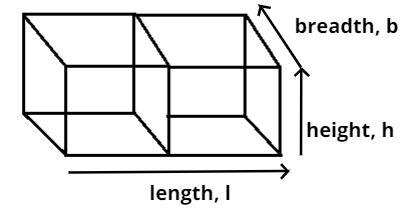
Given data volume of each cube = 64 $cm^2$.
Now as we know that volume (V) of the cube is the side cube.
Let the side of the cube be a cm.
$ \Rightarrow V = 64 = {a^3}$
$ \Rightarrow a = \sqrt[3]{{64}} = 4$ cm.
So the side of the cube is 4 cm.
Now two cubes are joined together as shown in figure to make a cuboid.
So as we see that the length (l) of the cuboid is double the side of the cube but breadth (b) and height (h) of the cuboid remain the same.
Therefore l = 2a, b = a and h = a cm.
Therefore l = 8 cm, b = 4 cm and h = 4 cm.
Now as we know that the surface area (S.A) of the cuboid is $2\left( {lb + bh + hl} \right)$.
$ \Rightarrow S.A = 2\left( {lb + bh + hl} \right) cm^2$.
\[ \Rightarrow S.A = 2\left( {\left( {8 \times 4} \right) + \left( {4 \times 4} \right) + \left( {4 \times 8} \right)} \right) = 2\left( {32 + 16 + 32} \right) = 2\left( {80} \right) = 160 cm^2\].
So this is the required surface area of the resulting cuboid.

Note – Cube is a symmetrical three dimensional shape, either solid or hollow contained by six equal squares thus combination of two cubes leads to formation of a cuboid. A cuboid has 6 faces so to find the surface area of a cuboid, add the areas of all the 6 faces, that’s why the formula for surface area $S.A = 2\left( {lb + bh + hl} \right)$.