Question

Two equal forces ($P$ each) act at a point inclined to each other at an angle of $120^\circ $. The magnitude of their resultant is:
A.)$\dfrac{P}{2}$
B.)$\dfrac{P}{4}$
C.)$P$
D.)$2P$

Answer 1

Hint – You can start the solution by drawing a well-labelled diagram with all the vectors ($P$, $P$ and the resultant) originating from a common point. The equations for the magnitude of the resultant vector and the direction of the resultant vector are $R = \sqrt {{A^2} + {B^2} + 2AB\operatorname{cos} \theta } $ and $\tan \alpha = \dfrac{{B\sin \theta }}{{A + B\cos \theta }}$ respectively. Use the first equation given above to reach the solution.

Step By Step Answer:
To solve this equation, consider the diagram given below

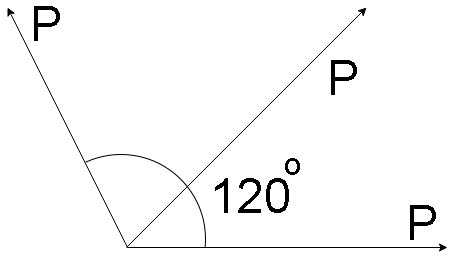
The arrangement of $P$, $P$ and $R$ (Resultant) vectors is done in such a way that it is easy to co-relate it with the other two vectors.

We know,

$R = \sqrt {{A^2} + {B^2} + 2AB\cos \theta } $, where $\theta $ is the angle between two vectors.
For this case

$R = \sqrt {{P^2} + {P^2} + 2PP\cos 120} $

\[ \Rightarrow R = \sqrt {{P^2} + {P^2} - {P^2}} \]
\[ \Rightarrow R = \sqrt {{P^2}} \]
\[ \Rightarrow R = P\]

Hence, Option C is the correct option

Additional Information:
A vector is a mathematical quantity that has both a magnitude (size) and a direction. To imagine what a vector is like, imagine asking someone for directions in an unknown area and they tell you, “Go $5km$ towards the West”. In this sentence, we see an example of a displacement vector, “\[5km\]” is the magnitude of the displacement vector and “towards the North” is the indicator of the direction of the displacement vector.
A vector quantity is different from a scalar quantity in the fact that a scalar quantity has only magnitude, but a vector quantity possesses both direction and magnitude. Unlike scalar quantities, vector quantities cannot undergo any mathematical operation, instead they undergo Dot product and Cross product.
Some examples of vectors are – Displacement, Force, Acceleration, Velocity, Momentum, etc.

Note – In such a type of question, it is very important to keep in mind what values you have to calculate. In this problem we only have to calculate the magnitude of the resultant vector. But the problem sometimes also asks for the angle it makes with the vectors and this can be done by using the formula \[\tan \alpha = \dfrac{{b\sin \theta }}{{a + b\cos \theta }}\], where \[a\] and \[b\] are the magnitude of the respective vectors.