Question

Two forces while acting on a particle in opposite direction having the resultant of 10 N. If they act at right angles to each other, the resultant is found to be 50 N. Find the two forces.

Answer 1

Hint: In order to solve this question we need to understand here that the two forces are acting at right angles to each other. Then it follows Parallelogram Law of Forces. Parallelogram Law of Forces states that Here, the two forces are acting at right angles to each other. Then it follows Parallelogram Law of Forces. Parallelogram Law of Forces states that Parallelogram Law of Forces.
 $ {a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2} $

Complete step by step answer:
 $ {\text{Let us consider the two forces be }}{F_1}{\text{ and }}{{\text{F}}_2}. $
It is given that the two forces are acting in opposite directions.

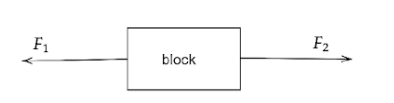
 $ {F_1} - {F_2} = 10{\text{ N - - - (1)}} $
And if the two forces are acting at right angles the resultant force is 50 N.

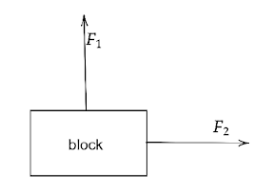
 $ \sqrt {{F_1}^2 + {F_2}^2} = 50{\text{ - - - (2)}} $
From equation (1), find the value of $ {F_1} $
 $ {F_1} = {F_2} + 10 $
Now, we know the value of $ {F_1} $
So, substitute the value of $ {F_1} $ in equation (2) to find the value of $ {F_2} $
 $ \Rightarrow {\left( {{F_2} + 10} \right)^2} + {\left( {{F_2}} \right)^2} = {50^2} $
Now use the $ {a^2} + 2ab + {b^2} = {\left( {a + b} \right)^2} $ for further solving.
 $ \Rightarrow \left[ {{{\left( {{F_2}} \right)}^2} + 100 + 20{F_2}} \right] + {\left( {{F_2}} \right)^2} = 2500 $
Now, arrange the variable and coefficients for solving.
 $ \Rightarrow 2{F_2}^2 + 20{F_2} = 2500 - 100 $
 $ \Rightarrow 2{F_2}^2 + 20{F_2} = 2400 $
Taking 2 common we get,
 $ \Rightarrow 2({F_2}^2 + 10{F_2}) = 2400 $
And dividing it by 2,
 $ \Rightarrow ({F_2}^2 + 10{F_2}) = \dfrac{{2400}}{2} $
 $ \Rightarrow ({F_2}^2 + 10{F_2}) = 1200 $
 $ \Rightarrow {F_2}^2 + 10{F_2} - 1200 = 0 $
Now, by using factoring method we get,
 $ \Rightarrow {F_2}^2 + 40{F_2} - 30{F_2} - 1200 = 0 $
Taking common,
 $ \Rightarrow {F_2}({F_2} + 40) - 30({F_2} + 40) = 0 $
 $ \Rightarrow ({F_2} + 40)({F_2} - 30) = 0 $
Here, we are getting two solutions for $ {F_2} $ . But the force acting on any object cannot be negative. So, the value of $ {F_2} $ is 30 N.
 $ \Rightarrow {F_2} = 30{\text{ N}} $
Now, we got the value of $ {F_2} $ force.
By substituting the value of $ {F_2} $ in equation (1) we get,
 $ \Rightarrow {F_1} - 40 = 10 $
 $ \Rightarrow {F_1} = 10 + 40{\text{ }} $
 $ \Rightarrow {F_1} = 40{\text{ N}} $ .

Note:
It should be remembered that the force is an interaction between two objects. Force is measured in Newton; one force interaction refers to one newton. The force acting on any object cannot be negative. If the force is acting in the opposite direction, then it means the difference between the two forces which is equal to the resultant force. If we substitute the value of $ {F_1} $ and $ {F_2} $ in equation (1) we will get the given resultant.