
Two glass plates are separated by water. If surface tension of water is
A.
B.
C.
D.
Answer
370.8k+ views
Hint: Use the excess pressure formula to find the pressure lowered between the plates i.e.
Here, T is the surface tension of water
R is the radius of the two surfaces due to which the pressure is lowered.
In simple words we will put the values in the equation to get the required force applied to separate the two plates.
Complete answer:
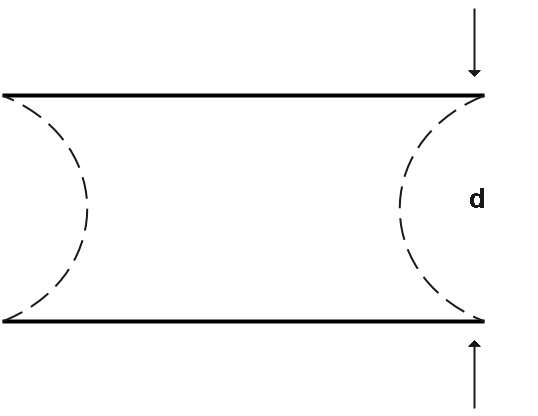
Here we can see the shape of the water layer between the two plates.
Thickness of the film,
Pressure of the cylindrical face,
Now, pressure across the surface,
Area of each plate wetted by water,
And we know that force required to separate the two plate is,
Now, substituting the values in above equation we get,
So, the force applied to separate the two plates is
Hence, the correct option is C.
Note:
Here the curved surface is a cylinder with radius R. Since this behaves as an air bubble in water that is why we have taken the radii to be equal. Otherwise, one should calculate the excess pressure using the radii of the given shape which is not a cylinder or spherical as an air bubble.
Here, T is the surface tension of water
R is the radius of the two surfaces due to which the pressure is lowered.
In simple words we will put the values in the equation to get the required force applied to separate the two plates.
Complete answer:

Here we can see the shape of the water layer between the two plates.
Thickness of the film,
Pressure of the cylindrical face,
Now, pressure across the surface,
Area of each plate wetted by water,
And we know that force required to separate the two plate is,
Now, substituting the values in above equation we get,
So, the force applied to separate the two plates is
Hence, the correct option is C.
Note:
Here the curved surface is a cylinder with radius R. Since this behaves as an air bubble in water that is why we have taken the radii to be equal. Otherwise, one should calculate the excess pressure using the radii of the given shape which is not a cylinder or spherical as an air bubble.
Recently Updated Pages
Master Class 11 Economics: Engaging Questions & Answers for Success

Master Class 11 Business Studies: Engaging Questions & Answers for Success

Master Class 11 Accountancy: Engaging Questions & Answers for Success

Master Class 11 English: Engaging Questions & Answers for Success

Master Class 11 Computer Science: Engaging Questions & Answers for Success

Master Class 11 Maths: Engaging Questions & Answers for Success

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




