Question

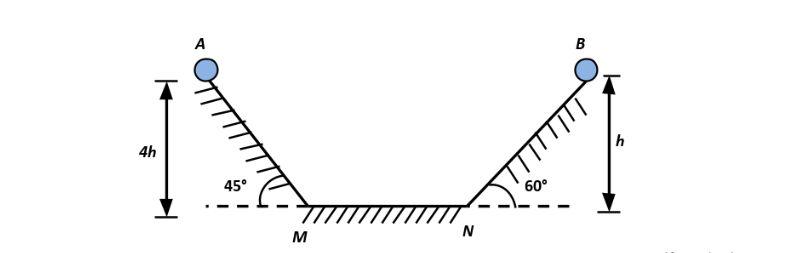
Two identical balls A and B are released from the positions shown in the figure. They collide
elastically on horizontal portion MN. The ratio of heights attained by A and B after collision will be
(neglect friction)

A. 1:4
B. 2:1
C. 4:13
D. 2:11

Answer 1

Hint:There are two balls that are identical, they have the same mass. Also, they collide
elastically. Then, by the conservation of momentum, the two balls of identical masses will just exchange their velocities when they collide.

Formula Used: The velocity of a ball at height \[h\] is \[v = \sqrt {2gh} \]
The maximum height attained by the ball in projectile motion is \[H = \dfrac{{{v^2}{{\sin }^2}\theta
}}{{2g}}\]

Complete step by step solution: In the diagram, two balls are given that are held at different heights. A ball that is held above the ground has a potential energy that is related to the height above which the object is held. And, if this object is dropped, the Kinetic energy will become the potential energy of motion. These Kinetic energies and potential energies are given by

\[KE = \dfrac{1}{2}m{v^2}\]and \[PE = mgh\] respectively, where \[m\]is the mass, \[v\]is the velocity
and \[h\] is the height of the ball. Thus, velocity of the ball can be calculated as follows

\[\dfrac{1}{2}m{v^2} = mgh \to {v^2} = \dfrac{{2mgh}}{m} = 2gh \to v = \sqrt {2gh} \] \[ \to (1)\]
Ball A has height \[4h\] and B has \[h\]. Let the velocity of ball A be \[{v_1}\] and that of ball B be
\[{v_2}\]. Thus, from equation (1)
\[{v_1} = \sqrt {2g(4h)} = \sqrt {8gh} \] and \[{v_2} = \sqrt {2gh} \]

It is given that the balls are identical and collide elastically, then their velocities will exchange. Now,
after collision, the balls will bounce backwards in the same direction from which they came with
exchanged velocities such that the velocity of ball A will be \[{v_2}\] and that of ball B will be \[{v_1}\].
When they bounce back, ball A will reach only upto height \[h\] on the \[4h\] heighted slant plane
because its velocity is \[{v_2}\] and it has potential only to reach the distance \[h\]. On the other hand, Ball B has potential to reach the distance \[4h\]. But, the slant plane has height \[h\]. Therefore, it will perform a projectile motion and will fall off the plane to the ground.

The angle of the second slant plane is given to be \[{60^ \circ }\]. Therefore, the ball B will be thrown off the plane making an angle \[{60^ \circ }\]. The total kinetic energy that ball B contains is
\[\dfrac{1}{2}m{v_1}^2\]. This energy can be resolved as
\[\dfrac{1}{2}m{v_1}^2 = mgh + \dfrac{1}{2}m{v^2}\] \[ \to (2)\]
where, \[mgh\]is the potential energy of the ball upto height \[h\]. Then, the ball will form a projectile.

Let the velocity of the ball while performing the projectile be \[v\]. Then the Kinetic energy will be
\[\dfrac{1}{2}m{v^2}\] as in equation (2).
Cancelling the mass of the ball from both the sides and substituting the value of \[{v_1}\], then equation(2) will be
\[\dfrac{1}{2}(8gh) = gh + \dfrac{1}{2}{v^2} \to {v^2} = 6gh \to v = \sqrt {6gh} \]
The velocity \[v = \sqrt {6gh} \] is the velocity for the projectile. The maximum height attained by ball B will be
\[H = \dfrac{{{v^2}{{\sin }^2}\theta }}{{2g}}\]
Here, \[\theta = {60^ \circ }\]. Therefore, \[H = \dfrac{{(6gh){{\sin }^2}({{60}^ \circ })}}{{2g}} = 3h
\times \dfrac{3}{4} = \dfrac{{9h}}{4}\]
Since, \[\sin {60^ \circ } = \dfrac{{\sqrt 3 }}{2} \to {\sin ^2}{60^ \circ } = \dfrac{3}{4}\]

The total height attained by ball B will be \[{h_B} = h + H = h + \dfrac{{9h}}{4} = \dfrac{{13h}}{4}\]
The ratio of heights attained by A and B after collision will be
\[\dfrac{{{h_A}}}{{{h_B}}} = \dfrac{h}{{\left( {\dfrac{{13h}}{4}} \right)}} = \dfrac{{4h}}{{13h}} =
\dfrac{4}{{13}}\]
Hence, option (C) is the correct answer.

Note: The balls should be identical in mass and radius with different velocities so that whenever they collide elastically, their velocities are exchanged. For example, two equal masses moving towards each other with equal speeds will stop dead when they collide. This is due to conservation of momentum.