Question

Two identical pith balls are charged by rubbing against each other. They are suspended from a horizontal rod through two strings of length 20 cm each, the separation between the suspension points being 5 cm. In equilibrium, the separation between the balls is 3 cm. Find the mass of each ball and the tension in the strings. The charge on each ball has a magnitude 2.0 x 10-8 C.

Answer 1

Hint: whenever two charged bodies are brought against each other and if they touch one another then redistribution of charge takes place until equilibrium is reached. If the shape and size of the two bodies is the same then the final charge on each of the bodies is equal. Here, the two bodies were charged by friction.

Complete step by step answer:

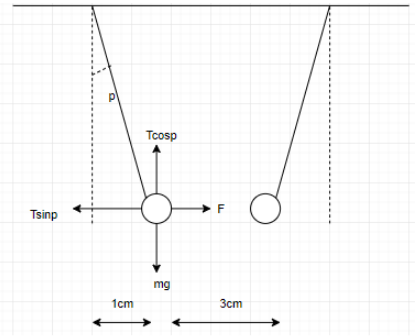
Length of rod= 20 cm, Separation between the equilibrium points= 5 cm.
Now when the equilibrium is reached, the separation becomes 3 cm, so,
\[q=2\times {{10}^{-8}}C\]
M=?
T=?
\[\sin \theta =\dfrac{1}{20}\]
We know Coulombic force is given by: \[F=\dfrac{k{{q}_{1}}{{q}_{2}}}{{{x}^{2}}}\]
where x is the distance between the two charges and k is the constant of proportionality.
Substituting the values, we get,
\[F=\dfrac{9\times {{10}^{9}}\times 2\times {{10}^{-8}}\times 2\times {{10}^{-8}}}{{{(3\times {{10}^{-2}})}^{2}}}\]
\[\Rightarrow\dfrac{9\times 4\times {{10}^{-7}}}{9\times {{10}^{-4}}}=4\times {{10}^{-3}}\]---(1)
Balancing the forces acting on the ball we get,
$mg\sin p=F \\
\Rightarrow m=\dfrac{F}{g\sin p} \\
\Rightarrow m=\dfrac{4\times {{10}^{-3}}\times 20}{10\times 1} \\
\Rightarrow m=8\times {{10}^{-3}} \\
\therefore m=8g \\$
So, the mass of each ball is 8g.
$\cos p=\sqrt{1-\dfrac{1}{400}} \\
\Rightarrow \cos p=\sqrt{\dfrac{399}{400}} \\
\Rightarrow \cos p=0.99 \\
\therefore \cos p\sim1 $
Thus, the tension developed is given as: T= mg cos p
$T=8\times {{10}^{-3}}\times 10\times 0.99 \\
\therefore T=0.08N$

So, the tension comes out to be 0.08 N.

Note: Here we have used the concept of equilibrium. When a number of forces acts on a body and then still the body remains at rest, then the vector sum of these forces comes out to be zero. Here the forces in the horizontal balance each other and the forces in the vertical do the same. When a body is hung from the vertical and if it is disturbed from its mean position then a force tends to bring it to the same.