Question

Two identical pith balls of mass m and having charge q are suspended from a point by weightless strings of length l. If both strings make an angle of $\theta $ with the vertical then the distance between the balls will be (Taking $\theta $ to be small).
A. ${{\left( \dfrac{{{q}^{2}}l}{2\pi {{\varepsilon }_{0}}mg} \right)}^{\dfrac{1}{3}}}$
B. ${{\left( \dfrac{{{q}^{2}}l}{4\pi {{\varepsilon }_{0}}mg} \right)}^{\dfrac{1}{3}}}$
C. ${{\left( \dfrac{q{{l}^{2}}}{4\pi {{\varepsilon }_{0}}mg} \right)}^{\dfrac{1}{3}}}$
D. ${{\left( \dfrac{q{{l}^{2}}}{2\pi {{\varepsilon }_{0}}mg} \right)}^{\dfrac{1}{3}}}$

Answer 1

Hint: When an object is at a steady-state it is known to be in equilibrium. Under this condition, all the forces acting on the body cancel out each other and the object remains in its mentioned position. When two charged bodies are kept at a distance they may pull or push each other depends on the type of field force they carry.

Complete answer:
When two objects are at a certain the force between them depends on the charge they carry and the distance between the two charges.
${{F}_{e}}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}_{1}}{{q}_{2}}}{{{r}^{2}}}$
According to the condition given in the question, two identical charges attached to a point with massless string are apart by a certain distance. This is shown in the diagram here,

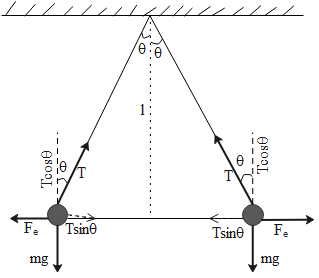
In equilibrium condition ,
The downward force will be equivalent to the upward force and the forward force will be equal to the backward force. So from the forces acting on the body as per the diagram shown above will be,
$\begin{align}
  & mg=T\cos \theta \quad ....(1) \\
 & {{F}_{e}}=T\sin \theta \quad ......(2) \\
\end{align}$
By putting the value of force (${{F}_{e}}$ ) in equation (2),
$\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{r}^{2}}}=T\sin \theta \quad ....(3)$
By equating equations (1) and (3),
$\begin{align}
  & \dfrac{T\sin \theta }{T\cos \theta }=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{r}^{2}}mg} \\
 & \Rightarrow \tan \theta =\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{r}^{2}}mg} \\
\end{align}$
By rearranging the distance between the two charges can be given as
$\begin{align}
  & \dfrac{r}{2l}=\dfrac{1}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{{{r}^{2}}mg} \\
 & \Rightarrow {{r}^{3}}=\dfrac{2l}{4\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{mg} \\
 & \Rightarrow r={{\left( \dfrac{l}{2\pi {{\varepsilon }_{0}}}\dfrac{{{q}^{2}}}{mg} \right)}^{\dfrac{1}{3}}} \\
\end{align}$
The value of $r$ can be written as,
$r={{\left( \dfrac{{{q}^{2}}l}{2\pi {{\varepsilon }_{0}}mg} \right)}^{\dfrac{1}{3}}}$

Thus the correct option for the question is Option A.

Note:
When any object is attached to a string with a certain angle a tension force acts along the string. The force is always directed from the free-moving object to the fixed point of the string. With the help of a free body diagram, all the forces acting on the body can be studied easily and estimations (calculations) become easier.