
Two independent harmonic oscillators of equal mass are oscillating about the origin with angular frequencies
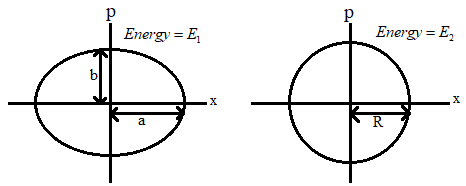
Answer
486.3k+ views
1 likes
Hint: We have two different particles undergoing independent harmonic oscillations and the mass of them are the same. We are given the angular frequencies and energies of the two systems. From the given figure we can identify their path and find the maximum momenta and their energies, then by using the given relations we will get the correct expressions.
Formula used:
Complete step-by-step answer:
In the question we are given two independent harmonic oscillations with equal mass.
The angular frequencies of the two oscillations are
Let us consider the first case.
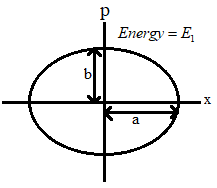
From the figure we can see that the particle in this oscillation has an elliptical path.
We know that the momentum is given by the equation,
Therefore the maximum momentum will be,
Since the maximum velocity,
Therefore in the first case, since it is an elliptical path the radius is taken as ‘a’ and from the figure we can see that ‘b’ is the maximum momentum.
Therefore we get,
Now let us consider case 2.
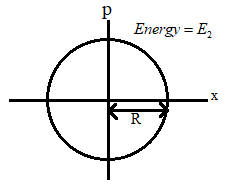
From the figure we can see that the particle in this oscillation has a circular path.
We know that the maximum momentum is,
In this case, from the figure we can see that the radius and the maximum momentum is ‘R’. therefore we get,
Thus we have the maximum momentum in case 1 and 2 as
By dividing these two equations we get,
Since the mass is equal in both the cases. We can eliminate the mass.
In the question it is given that
Therefore we know that,
By substituting this we will get,
Therefore we get,
Hence option B is correct.
Now let us consider the energy in both the cases.
In the first case, we will get the energy as,
By dividing these two equations, we will get
From the question we know that,
Therefore we know that
Thus the ratio of the energies will become,
From previous calculation we know that,
By substituting this in the ratio equation, we will get
Therefore option D is also correct.
So, the correct answer is “Option B and D”.
Note: A periodic oscillation is an oscillation when the periodic motion repeats at fixed intervals. Simple harmonic motion or SHM is a special type of periodic oscillation. In simple harmonic motion the restoring force of the moving object will be always directly proportional to the magnitude of displacement of the object and its direction will be toward the mean position.
Formula used:
Complete step-by-step answer:
In the question we are given two independent harmonic oscillations with equal mass.
The angular frequencies of the two oscillations are
Let us consider the first case.

From the figure we can see that the particle in this oscillation has an elliptical path.
We know that the momentum is given by the equation,
Therefore the maximum momentum will be,
Since the maximum velocity,
Therefore in the first case, since it is an elliptical path the radius is taken as ‘a’ and from the figure we can see that ‘b’ is the maximum momentum.
Therefore we get,
Now let us consider case 2.

From the figure we can see that the particle in this oscillation has a circular path.
We know that the maximum momentum is,
In this case, from the figure we can see that the radius and the maximum momentum is ‘R’. therefore we get,
Thus we have the maximum momentum in case 1 and 2 as
By dividing these two equations we get,
Since the mass is equal in both the cases. We can eliminate the mass.
In the question it is given that
Therefore we know that,
By substituting this we will get,
Therefore we get,
Hence option B is correct.
Now let us consider the energy in both the cases.
In the first case, we will get the energy as,
By dividing these two equations, we will get
From the question we know that,
Therefore we know that
Thus the ratio of the energies will become,
From previous calculation we know that,
By substituting this in the ratio equation, we will get
Therefore option D is also correct.
So, the correct answer is “Option B and D”.
Note: A periodic oscillation is an oscillation when the periodic motion repeats at fixed intervals. Simple harmonic motion or SHM is a special type of periodic oscillation. In simple harmonic motion the restoring force of the moving object will be always directly proportional to the magnitude of displacement of the object and its direction will be toward the mean position.
Latest Vedantu courses for you
Grade 9 | CBSE | SCHOOL | English
Vedantu 9 CBSE Pro Course - (2025-26)
School Full course for CBSE students
₹37,300 per year
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




