Question

Two intersecting circles have their radius 1 and $\sqrt{3}$ metres. The distance between their centres is 2 metres, Then, the overlapping area in sq. metres is
a). $\dfrac{19\pi +6\sqrt{3}}{6}$
b). $\dfrac{5\pi +6\sqrt{3}}{6}$
c). $\dfrac{\pi }{6}$
d). $\dfrac{5\pi -6\sqrt{3}}{6}$

Answer 1

Hint: We will first recall the properties of the circle to find the overlapping area of the circles. At first we will find the area of both the arc formed due to overlapping circle portions and then we will find the area of both triangles which is formed due to the common chord of overlapping circles. And, we know that the common chord divides the overlapping portion into two parts, so we will then find the both the parts by subtracting the area of the arc with the area of the corresponding triangle and then add the area of both the parts to get the area of the overlapping portion.

Complete step by step answer:
We will use the properties of the circle to solve the above question. Let us first assume two overlapping circles as ${{C}_{1}}$ and ${{C}_{2}}$ whose centre are A and B, and let 1 be the radius of circle ${{C}_{1}}$ and $\sqrt{3}$ be the radius of the circle ${{C}_{2}}$ and let EF be the common chord of both the circle and AB is line joining centre of both the circle. So, radius AE = 1 and radius BE = $\sqrt{3}$

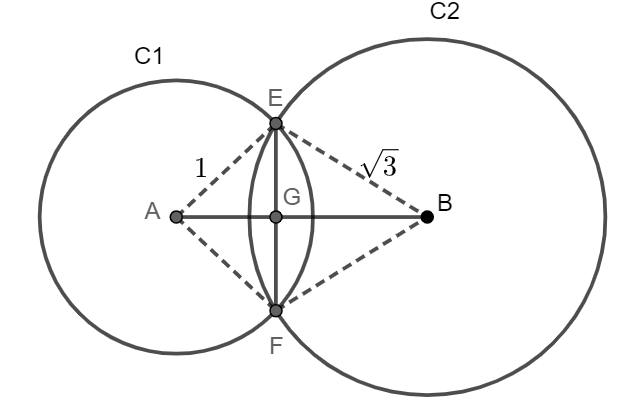
Now, from properties of the circle we know that the line joining the centres of two overlapping circles is a perpendicular bisector of their common chord. So, we can say that AB is the perpendicular bisector of EF and bisects it at G. So, we can say that EG = GF.
Now, let us assume that length of the common chord is x metres i.e. EF = x:
And , we can see from figure that EF = EG + GF = x
Also, EF = GF
So, we can write EG + EG = x.
$\Rightarrow EG=\dfrac{x}{2}=GF$
Now, in right triangle $\Delta AGE$, we can write:
${{\left( AE \right)}^{2}}={{\left( AG \right)}^{2}}+{{\left( EG \right)}^{2}}$ , by Pythagoras Theorem
We know that AE = 1, and $EG=\dfrac{x}{2}$
$\Rightarrow AG=\sqrt{A{{E}^{2}}-E{{G}^{2}}}$
$\Rightarrow AG=\sqrt{{{1}^{2}}-{{\left( \dfrac{x}{2} \right)}^{2}}}$
$\therefore AG=\sqrt{\dfrac{4-{{x}^{2}}}{4}}=\dfrac{\sqrt{4-{{x}^{2}}}}{2}----(1)$
Now, in right triangle $\Delta BGE$ , we can write:
${{\left( BE \right)}^{2}}={{\left( BG \right)}^{2}}+{{\left( EG \right)}^{2}}$ , by Pythagoras Theorem
We know that BE = $\sqrt{3}$, and $EG=\dfrac{x}{2}$
$\Rightarrow BG=\sqrt{B{{E}^{2}}-E{{G}^{2}}}$
$\Rightarrow BG=\sqrt{{{\left( \sqrt{3} \right)}^{2}}-{{\left( \dfrac{x}{2} \right)}^{2}}}$
$\therefore BG=\sqrt{\dfrac{12-{{x}^{2}}}{4}}=\dfrac{\sqrt{12-{{x}^{2}}}}{2}---(2)$
So, the distance between the centres A and B = AB = AG + BG
$\Rightarrow AB=\dfrac{\sqrt{4-{{x}^{2}}}}{2}+\dfrac{\sqrt{12-{{x}^{2}}}}{2}$ , from (1) and (2)
We know from question that AB = 2 metres
So, we can write:
$\Rightarrow AB=\dfrac{\sqrt{4-{{x}^{2}}}}{2}+\dfrac{\sqrt{12-{{x}^{2}}}}{2}=2$
$\Rightarrow \sqrt{4-{{x}^{2}}}+\sqrt{12-{{x}^{2}}}=2\times 2$
$\begin{align}
  & \Rightarrow \sqrt{4-{{x}^{2}}}+\sqrt{12-{{x}^{2}}}=4 \\
 & \Rightarrow \sqrt{12-{{x}^{2}}}=4-\sqrt{4-{{x}^{2}}} \\
\end{align}$
Now, after squaring both sides we will get:
$\begin{align}
  & \Rightarrow {{\left( \sqrt{12-{{x}^{2}}} \right)}^{2}}={{\left( 4-\sqrt{4-{{x}^{2}}} \right)}^{2}} \\
 & \Rightarrow 12-{{x}^{2}}=16+4-{{x}^{2}}-2\times 4\times \sqrt{4-{{x}^{2}}} \\
 & \Rightarrow 12=20-8\times \sqrt{4-{{x}^{2}}} \\
 & \Rightarrow 8\times \sqrt{4-{{x}^{2}}}=8 \\
 & \Rightarrow \sqrt{4-{{x}^{2}}}=1 \\
\end{align}$
Now, again after squaring both sides we will get:
$\Rightarrow 4-{{x}^{2}}=1$
$\Rightarrow {{x}^{2}}=3$
$\Rightarrow x=\sqrt{3}-----(3)$
 So, the length of the common chord is $\sqrt{3}$.
So, we can say that $EG=GF=\dfrac{x}{2}=\dfrac{\sqrt{3}}{2}$
Now, in right triangle $\Delta BGE$:
$\sin \left( \angle GBE \right)=\dfrac{GE}{BE}$ , because $\sin \theta =\dfrac{perpendicular}{base}$
 $\sin \left( \angle GBE \right)=\dfrac{\dfrac{\sqrt{3}}{2}}{\sqrt{3}}$
$\sin \left( \angle GBE \right)=\dfrac{1}{2}$
We know from trigonometric table that $\sin \theta =\dfrac{1}{2}$, is possible only when $\theta =30{}^\circ $
So, $\angle GBE=30{}^\circ $
Now, in right triangle $\Delta AGE$:
$\sin \left( \angle GAE \right)=\dfrac{GE}{AE}$ , because $\sin \theta =\dfrac{perpendicular}{base}$

$\sin \left( \angle GAE \right)=\dfrac{\dfrac{\sqrt{3}}{2}}{1}$
$\sin \left( \angle GAE \right)=\dfrac{\sqrt{3}}{2}$
We know from trigonometric table that $\sin \theta =\dfrac{\sqrt{3}}{2}$, is possible only when $\theta =60{}^\circ $
So, $\angle GAE=60{}^\circ $
Now, we know that a line joining the centres of two overlapping circles divides the angle subtended by their common chord at the centre into two equal halves.
So, we can say that $\angle EBG=\angle FBG$ and $\angle EAG=\angle FAG$.
Now, in triangle $\Delta EAF$:
$\begin{align}
  & \Rightarrow \angle EAF=\angle EAG+\angle FAG \\
 & \Rightarrow \angle EAF=\angle EAG+\angle EAG \\
 & \Rightarrow \angle EAF=2\angle EAG \\
 & \Rightarrow \angle EAF=2\times 60{}^\circ \\
 & \therefore \angle EAF=120{}^\circ \\
\end{align}$
Similarly, in triangle $\Delta EBF$:
$\begin{align}
  & \Rightarrow \angle EBF=\angle EBG+\angle FBG \\
 & \Rightarrow \angle EBF=\angle EBG+\angle EBG \\
 & \Rightarrow \angle EBF=2\angle EBG \\
 & \Rightarrow \angle EBF=2\times 30{}^\circ \\
 & \therefore \angle EBF=60{}^\circ \\
\end{align}$
Now, we will find the area of the arc EAFE.
We know that area of the arc is given $\pi {{r}^{2}}\times \dfrac{\theta }{360{}^\circ }$ , where r is the radius of the arc and $\theta $ is the angle subtended by the arc at the centre.
So, area of arc EAFE which subtend an angle of $120{}^\circ $at the centre, and radius is 1 meter is equal to:
$\Rightarrow $ area of the arc EAFE = $\pi \times {{\left( 1 \right)}^{2}}\times \dfrac{120{}^\circ }{360{}^\circ }{{m}^{2}}$
$\Rightarrow $ area of the arc EAFE = $\pi \times \dfrac{1}{3}$ = $\dfrac{\pi }{3}{{m}^{2}}---(4)$
Now, we find the area of arc EBFE.
So, area of arc EBFE which subtend an angle of $60{}^\circ $at the centre, and radius is $\sqrt{3}$ meter is equal to:
$\Rightarrow $ area of the arc EAFE = $\pi \times {{\left( \sqrt{3} \right)}^{2}}\times \dfrac{60{}^\circ }{360{}^\circ }{{m}^{2}}$
$\Rightarrow $ area of the arc EAFE = $\pi \times 3\times \dfrac{1}{6}{{m}^{2}}$ = $\dfrac{\pi }{2}{{m}^{2}}---(5)$
Now, since the chord EF divides the overlapping area into two parts.
So, \[\text{area of arc EAFE }\text{ area of }\Delta EAF\] gives the area of the first part of the overlapped area.
And, \[\text{area of arc EBFE }\text{ area of }\Delta EBF\] gives the area of the second part of the overlapped area.
So, we will find the area of the triangle $\Delta EAF$:
$\Rightarrow \text{Area of }\Delta EAF=\dfrac{1}{2}\times AG\times EF$
Since, we have assumed previously we have assumed that EF = x and from (1) we know that $AG=\dfrac{\sqrt{4-{{x}^{2}}}}{2}$ which is perpendicular bisector of EF.
So, area of $\Delta EAF$= $\dfrac{1}{2}\times \dfrac{\sqrt{4-{{x}^{2}}}}{2}\times x$
From (3) we know that $x=\sqrt{3}m$ .
$\begin{align}
  & \Rightarrow \text{Area of }\Delta EAF=\dfrac{1}{2}\times \dfrac{\sqrt{4-{{\left( \sqrt{3} \right)}^{2}}}}{2}\times \sqrt{3}{{m}^{2}} \\
 & \Rightarrow \text{Area of }\Delta EAF=\dfrac{1}{2}\times \dfrac{1}{2}\times \sqrt{3}{{m}^{2}} \\
 & \Rightarrow \text{Area of }\Delta EAF=\dfrac{\sqrt{3}}{4}{{m}^{2}}---(6) \\
\end{align}$
Similarly, we will find the area of $\Delta EBF$:
$\Rightarrow \text{Area of }\Delta EBF=\dfrac{1}{2}\times BG\times EF$
Since, we have assumed previously we have assumed that EF = x and from (2) we know that $BG=\dfrac{\sqrt{12-{{x}^{2}}}}{2}$ which is perpendicular bisector of EF.
So, area of $\Delta EBF$= $\dfrac{1}{2}\times \dfrac{\sqrt{12-{{x}^{2}}}}{2}\times x$
From (3) we know that $x=\sqrt{3}m$ .
$\begin{align}
  & \Rightarrow \text{Area of }\Delta EBF=\dfrac{1}{2}\times \dfrac{\sqrt{12-{{\left( \sqrt{3} \right)}^{2}}}}{2}\times \sqrt{3}{{m}^{2}} \\
 & \Rightarrow \text{Area of }\Delta EBF=\dfrac{1}{2}\times \dfrac{3}{2}\times \sqrt{3}{{m}^{2}} \\
 & \Rightarrow \text{Area of }\Delta EBF=\dfrac{3\sqrt{3}}{4}{{m}^{2}}---(7) \\
\end{align}$
Now, since the chord EF divide the overlapping area into two parts.
So, \[\text{area of arc EAFE }\text{ area of }\Delta EAF\] gives the area of the first part of the overlapped area.
Area of first part of the overlapped area = \[\text{area of arc EAFE }\text{ area of }\Delta EAF\]
We know from (4) that area of the arc EAFE = $\pi \times \dfrac{1}{3}$ = $\dfrac{\pi }{3}{{m}^{2}}$ and (6) that area of the $\Delta EAF$ is $\dfrac{\sqrt{3}}{4}{{m}^{2}}$.
$\Rightarrow $ Area of first part of the overlapped area = $\dfrac{\pi }{3}{{m}^{2}}-\dfrac{\sqrt{3}}{4}{{m}^{2}}$.
And, \[\text{area of arc EBFE }\text{ area of }\Delta EBF\] gives the area of the second part of the overlapped area.
We know from (5) that area of the arc EBFE = $\pi \times \dfrac{1}{2}$ = $\dfrac{\pi }{2}{{m}^{2}}$ and (7) that area of the $\Delta EBF$ is $\dfrac{3\sqrt{3}}{4}{{m}^{2}}$.
$\Rightarrow $ Area of first part of the overlapped area = $\dfrac{\pi }{2}{{m}^{2}}-\dfrac{3\sqrt{3}}{4}{{m}^{2}}$
Hence, total area of the overlapped part = area of first part + area of second part
$\begin{align}
  & \Rightarrow \dfrac{\pi }{3}{{m}^{2}}-\dfrac{\sqrt{3}}{4}{{m}^{2}}+\dfrac{\pi }{2}{{m}^{2}}-\dfrac{3\sqrt{3}}{4}{{m}^{2}} \\
 & \Rightarrow \left( \dfrac{3\pi +2\pi }{6}-\dfrac{4\sqrt{3}}{4} \right){{m}^{2}} \\
 & \Rightarrow \left( \dfrac{5\pi }{6}-\sqrt{3} \right){{m}^{2}} \\
 & \Rightarrow \left( \dfrac{5\pi -6\sqrt{3}}{6} \right){{m}^{2}} \\
\end{align}$
Hence, overlapped area = $\left( \dfrac{5\pi -6\sqrt{3}}{6} \right){{m}^{2}}$

Hence, option (d) is our required answer.

Note:
Students are required to memorize all the properties of the circle and also the Pythagoras theorem and area of arc and triangle formula which is required many times and they should not make any calculation mistakes as the solution is a little bit lengthy.