Question

Two lines that intersect each other at right angles are called \[\]
A. Parallel \[\]
B. Perpendicular \[\]
C. Equal \[\]
D. None of these \[\]

Answer 1

Hint: We recall the definition of right angle, intersecting lines, and the angle they subtended at the point of intersection, parallel lines, and angle between them, and whether equality can be established between lines. We use the definition that these lines are perpendicular if they divide the straight angle subtended at the other line equally.

Complete step-by-step solution
We know a straight line is a one-dimensional geometrical shape with no curvature extended in two directions as a collection of points. A line is denoted with two points $A, B$ on the line as $\overleftrightarrow{AB}$, or by a single letter $l.$ We know that a line subtends a straight angle which is defined as an angle with a measure of ${{180}^{\circ }}$at any point $O.$ So we have $\angle AOB={{180}^{\circ }}$ \[\]

We know that two lines can at most intersect at one point or do not intersect at all. When they intersect they are called intersecting lines and if they do not they are called parallel lines. The angle between parallel lines is ${{0}^{\circ }}$or ${{180}^{\circ }}$. So option A is not correct. \[\]
Let us have two lines $\overleftrightarrow{AB}$ and $\overleftrightarrow{CD}$ intersect each other at the point $O$.We have the figure as \[\]
 

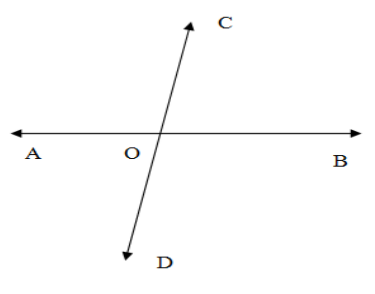
The lines $\overleftrightarrow{AB}, ,\overleftrightarrow{CD}$ are perpendicular if they divide the straight angle subtended at the other line equally. $\overleftrightarrow{CD}$ divides the straight angle $\angle AOB$ into angles $\angle AOC,\angle BOC$ above itself and into angles $\angle AOD,\angle BOD$ below itself. If they intersect each other at right angle as given in the question which means they at intersect with angle with measurement ${{90}^{\circ }}$, then we have,
\[\begin{align}
  & \angle AOC=\angle BOC={{90}^{\circ }} \\
 & \angle AOD=\angle BOD={{90}^{\circ }} \\
\end{align}\]
Let us add then and get
\[\begin{align}
  & \angle AOC+\angle BOC={{90}^{\circ }}+{{90}^{\circ }}=\angle AOB \\
 & \angle AOD+\angle BOD={{90}^{\circ }}+{{90}^{\circ }}=\angle AOB \\
\end{align}\]
So the $\overleftrightarrow{AB}, \overleftrightarrow{CD}$ divide the straight angle at the other line into two congruent right angles, and hence they are perpendicular. So option B is correct.\[\]
 

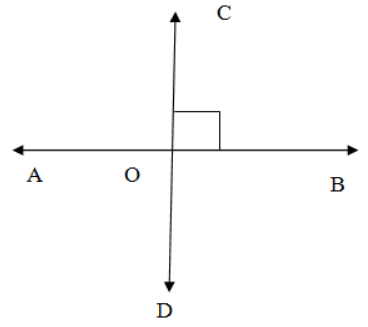
We know that lines cannot be measured but segments of the line can be measured. So option C is incorrect.\[\]

Note: We note that when two lines intersect they subtend pairs of two equal angles at the opposite of a line are called vertically opposite angles. Here the vertically opposite angles are $\angle AOC,\angle BOD$ and $\angle BOC,\angle AOD.$ The angels who are on the same side are called linear pairs. Here the linear pairs at the same side of $\overleftrightarrow{AB}$ are $\left( \angle AOC,\angle BOC \right)$ and $\left( \angle AOD,\angle BOD \right)$ . The linear pairs at the same side of $\overleftrightarrow{CD}$ are $\left( \angle BOC,\angle BOD \right)$ and $\left( \angle AOC,\angle AOD \right)$ . The examples of perpendicular lines are coordinate axes in-plane, sides of rectangle, diameter, and tangent of the circle, etc.