Question

Two long conductors, separated by a distance d carry currents $I_1$ and $I_2$ in the same direction. They exert a force F on each other. Now the current in one of them is increased to two times and its direction is reversed. The distance is also increased to 3 times. The new value of the force between them is:
A.$-\dfrac{2F}{3}$
B.$\dfrac{F}{3}$
C.$-2F$
D.$-\dfrac{F}{3}$

Answer 1

Hint: We know that every current carrying conductor produces a magnetic field which exerts a force on a neighbouring conductor. This force is directly proportional to the current carried by the conductors and its strength decreases with an increase in distance between the two. In such a case, obtain an expression for F that they initially exert on each other. Then, use the change in the parameters to obtain a subsequent expression for the new force exerted between them in terms of the initial force, which is what we require to this end. Use the right hand rule to determine the direction of the force in any case.
Formula Used:
Force exerted per unit length $ F = B\times I_2 = \dfrac{\mu_0 I_1I_2}{2 \pi d}$

Complete answer:
We have two long current carrying conductors oriented as shown in the diagram.

Let us begin with the foundation that a current carrying conductor produces a magnetic field.
We see that the magnetic field produced by one straight conductor will exert a force on the other conductor, and the other conductor does the same in such a way that there is a mutual force that is exerted between the two current carrying conductors. The magnitude of this force acting per unit length of the conductor depends on the strength of the magnetic field. The strength of this magnetic field is proportional to the current flowing through the conductor and gets weaker with distance from the wire, i.e.,
$\vec{B} \propto \dfrac{i}{2\pi d} \Rightarrow \vec{B} = \dfrac{\mu_0i}{2\pi d}$, where $\mu_0$ is the proportionality constant which is the magnetic permeability of free space.
The direction of the magnetic force between the two conductors can be found using the right hand rule, and is directed as shown in the diagram.
The force exerted by the first conductor on the second will be:
$\vec{F_{12}} = \vec{B_1}\times I_2 = \dfrac{\mu_0 I_1 I_2}{2\pi d}$
$\vec{F_{21}} = \vec{B_2}\times I_1 = \dfrac{\mu_0 I_2 I_1}{2\pi d}$
$\Rightarrow \vec{F_{12}} =\dfrac{\mu_0 I_1 I_2}{2\pi d}= \vec{F_{21}} = \vec{F} $.
Now, let us look at the second case, where current is reversed and $I^{\prime}_2 = 2I_2$ and $d^{\prime} = 3d$.

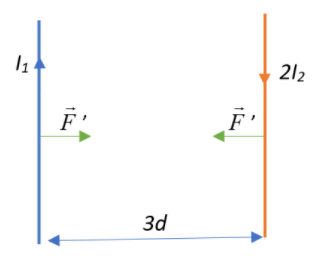
Since the current is reversed, we can deduce from the right hand thumb rule that the direction of the magnetic field produced by the second conductor will be opposite, and the new force exerted between the two conductors can be given as:
$F^{\prime} =\vec{F_{21}} = -\vec{B_2}\times I_1 = -\dfrac{\mu_0 I_1 2I_2}{2\pi 3d} = -\dfrac{2}{3}. \dfrac{\mu_0 I_1 I_2}{2\pi d} = -\dfrac{2F}{3}$

Therefore, the correct choice would be A. $-\dfrac{2F}{3}$

Note:
Do not get confused between the right hand rule and the right hand thumb rule.
The right hand rule involves using three fingers aligned in perpendicular directions to each other, where the magnetic force (indicated by thumb), the moving charge or current (indicated by index finger) and the magnetic field direction (indicated by the middle finger) can be determined.
The right hand “thumb” rule involves a closed fist, with the upright thumb pointing in the direction of current flow and the fist representing the direction of the magnetic field lines.
The magnetic force exerted by a conductor is always directed perpendicular to both the flow of current and the magnetic field produced.