Question

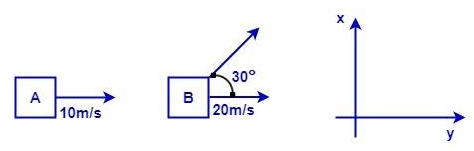
Two objects A and B are moving along the directions as shown in the figure. Find the magnitude and direction of the relative velocity of B w.r.t. A.

Answer 1

Hint Relative velocity of B w.r.t. A is given by:
 $\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}} $
Magnitude of this relative velocity is $ \left| \overrightarrow{{{v}_{BA}}} \right| $
Direction of this relative velocity is given by the angle $ \alpha $ which is calculated by:
 $\Rightarrow \tan \alpha =\frac{{{v}_{B{{A}_{y}}}}}{{{v}_{B{{A}_{x}}}}} $
Where $ {{v}_{B{{A}_{y}}}} $ and $ {{v}_{B{{A}_{x}}}} $ are the y and x components of $ \overrightarrow{{{v}_{BA}}} $ .

Complete step by step solution
 $ \begin{align}
  &\Rightarrow \overrightarrow{{{v}_{A}}}=10\widehat{i} \\
 &\Rightarrow \text{Here taking the components of velocity of B;} \\
 &\Rightarrow \overrightarrow{{{v}_{B}}}=20\cos 30{}^\circ \widehat{i}+20\sin 30{}^\circ \widehat{j} \\
 &\Rightarrow10\sqrt{3}\widehat{i}+10\widehat{j} \\
\end{align} $
Relative velocity of B w.r.t. A is
 $ \begin{align}
 &\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}-\overrightarrow{{{v}_{A}}} \\
 &\Rightarrow =10\sqrt{3}\widehat{i}+10\widehat{j}-10\sqrt{3}\widehat{i} \\
 &\Rightarrow =10\left( \sqrt{3}-1 \right)\widehat{i}+10\widehat{j} \\
\end{align} $
 $ \begin{align}
  & Now \\
 &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}+{{1}^{2}}} \\
 &\Rightarrow10\sqrt{3+1-2\sqrt{3}+1} \\
 &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{5-2\sqrt{3}}m{{s}^{-1}} \\
 & \text{For direction;} \\
 &\Rightarrow \tan \alpha =\frac{10}{10\left( \sqrt{3}-1 \right)} \\
 &\Rightarrow \tan \alpha =\frac{1}{\sqrt{3}-1} \\
 &\Rightarrow \alpha ={{\tan }^{-1}}\left( \frac{1}{\sqrt{3}-1} \right) \\
\end{align} $ .

Note
Alternate method:
Velocity of B w.r.t. A:
 $\Rightarrow \overrightarrow{{{v}_{BA}}}=\overrightarrow{{{v}_{B}}}+\left( -\overrightarrow{{{v}_{A}}} \right) $

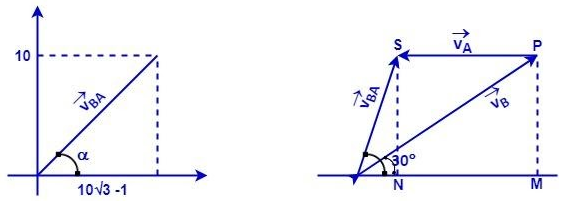
From the figure;
 $ \begin{align}
 &\Rightarrow NS=MP=20\sin 30{}^\circ \\
 &\Rightarrow NS=10 \\
 & and \\
 &\Rightarrow ON=OM-NM \\
 &\Rightarrow ON=20\cos 30{}^\circ -10 \\
 &\Rightarrow ON=10\left( \sqrt{3}-1 \right) \\
 &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=\sqrt{O{{N}^{2}}+N{{S}^{2}}} \\
 &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{{{\left( \sqrt{3}-1 \right)}^{2}}+{{1}^{2}}} \\
 &\Rightarrow \left| \overrightarrow{{{v}_{BA}}} \right|=10\sqrt{5-2\sqrt{3}}m{{s}^{-1}} \\
\end{align} $
 $ \begin{align}
 & \text{For direction;} \\
 &\Rightarrow \text{tan }\alpha =\frac{NS}{ON} \\
 &\Rightarrow \tan \alpha =\frac{10}{10\left( \sqrt{3}-1 \right)} \\
 &\Rightarrow \tan \alpha =\frac{1}{\sqrt{3}-1} \\
 &\Rightarrow \alpha ={{\tan }^{-1}}\left( \frac{1}{\sqrt{3}-1} \right) \\
\end{align} $ .