Question

Two objects, each are having a mass of $1.5kg$, are moving in the same straight line but in opposite directions. The velocity of each of the objects is $2.5m{{s}^{-1}}$and after the collision during which they stick together. What will be the velocity of the combined mass when they stick together after collision?

Answer 1

Hint: The law of conservation of momentum is used here. The momentum should be conserved before and after the collision. After the collision, the masses will stick together. Therefore combined mass of the system should be considered. These all may help you to solve the question.

Complete answer:
First of all let us look at what all are given in the question,
The mass of the two objects are equal, therefore we can write that,
${{m}_{1}}={{m}_{2}}=1.5kg$
And also the velocity before the collision for each of the object is,
${{u}_{1}}={{u}_{2}}=2.5m{{s}^{-1}}$
As per the question, the masses will stick together after the collision takes place, therefore when we calculate the momentum after the collision, the combined mass of the whole system should be taken.
Therefore the combined mass of the objects will be,
$M={{m}_{1}}+{{m}_{2}}=2\times 1.5=3kg$
Let us assume that the velocity of the mass after the collision as $v$,
According to the conservation of linear momentum, we can write that the momentum before the collision will be equivalent to the momentum after the collision.

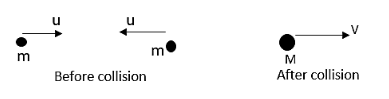
Therefore we can write that,
${{m}_{1}}{{u}_{1}}-{{m}_{2}}{{u}_{2}}=Mv$
Substituting the values in the equation will give,
$1.5\times 2.5-1.5\times 2.5=3v$
Simplifying the equation will give,

$\begin{align}
  & 3v=0 \\
 & \therefore v=0m{{s}^{-1}} \\
\end{align}$

Note:
Isaac Newton is the founder of the law of conservation of momentum. He discovered this when he made the laws of motion. In an isolated system like the universe, if there are no external forces acting, then the momentum is conserved every time. It is because when momentum is conserved, the components in any of the directions will also be conserved.