
Two parabolas
(a) their tangents at P make Complementary angle with x-axis.
(b) they touch each other at P.
(c) they intersect at right angles at P.
(d) None of these.
Answer
475.2k+ views
Hint: We start solving the problem by finding the point of intersection of the parabolas other than the origin. We then find the slope of the tangents for both the parabolas at the point P using the fact that the slope of the tangent for a conic is defined as
Complete step by step answer:
According to the problem, we are given that two parabolas
Let us find the intersection point P of the parabolas
Let us substitute
So, we get
So, the intersection point P is
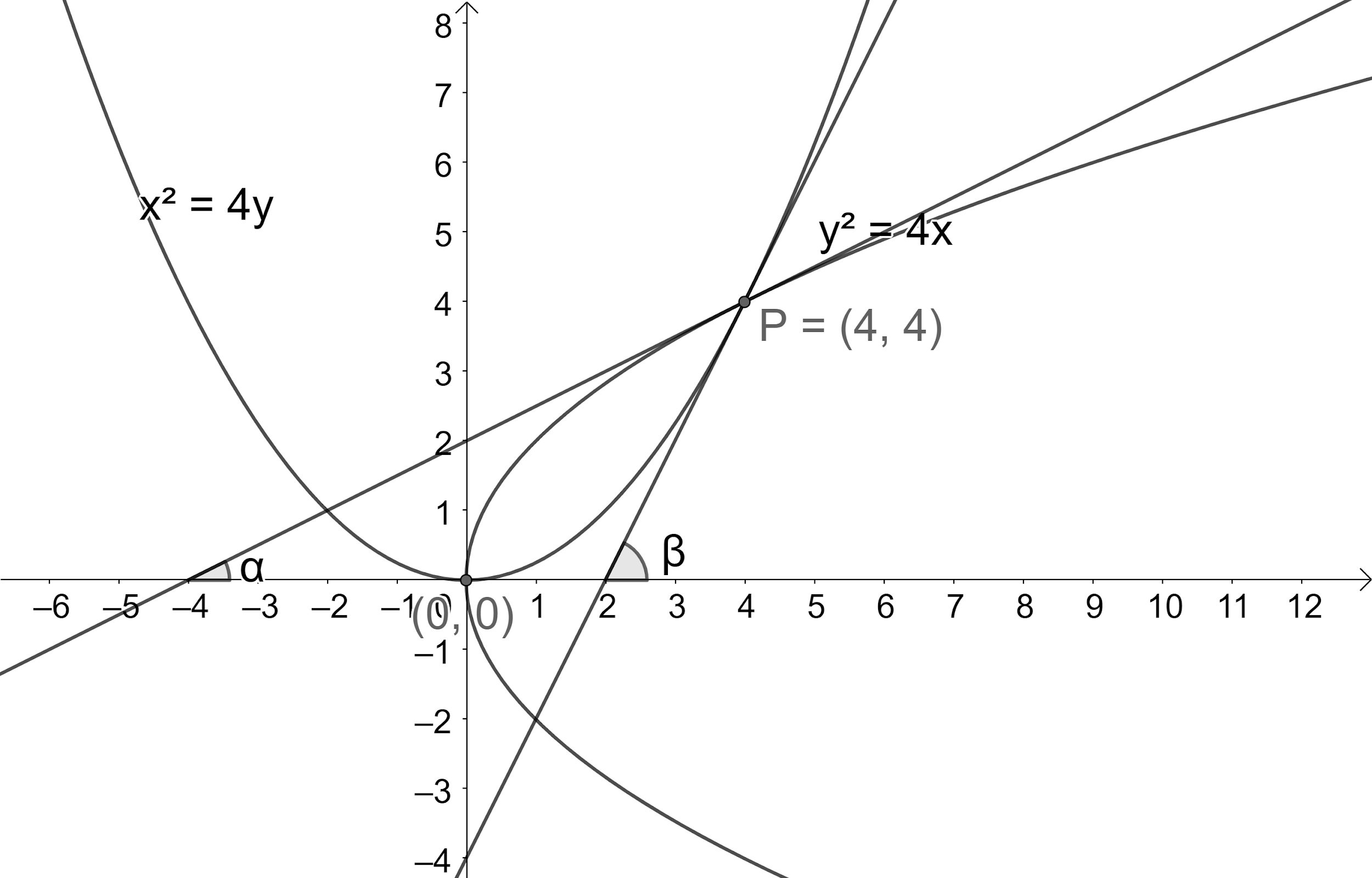
Let us find the slope of the tangent to parabola
We know that the slope of the tangent at any point for a conic is defined as
Let us differentiate
So, we get
Now, let us find the slope of the tangent to parabola
Let us differentiate
So, we get
We know that if the two parabolas touch each other at a point, then they will have a common tangent at that point. This means that the slope of both the tangents should be equal.
From equation (1) and (2), we can see that the slopes are equal which means that the parabolas are not touching each other at point P.
We know that if the two parabolas are perpendicular to each other at a point, then they will have a perpendicular tangent at that point. This means that the product of slopes of both the tangents should be equal to ‘–1’.
Let us multiply the slopes obtained in equation (1) and (2). So, we get
Now, let us find the angles made by each tangent with x-axis.
We know that the slope of any line is equal to the tangent of the angle made by a line with x-axis.
Let us assume the angles made by these two tangents with x-axis be
So, we have
And
Let us add the angles
We have
We know that
So, we get
We know that the sum of two complementary angles is
So, the tangents of both the parabolas at point P make complementary angles with x-axis.
So, the correct answer is “Option a”.
Note: We can see that the given problem contains a heavy amount of calculation, so we need to avoid calculation mistakes while solving this problem. We can also find the equation of the tangents at the point of the intersection P using the slope of each of the tangents. We should not consider the value of x which may give origin as the intersection as it is clearly mentioned in the problem. Similarly, we can expect problems to find the sum of the angles made by normal at this point with x-axis.
Complete step by step answer:
According to the problem, we are given that two parabolas
Let us find the intersection point P of the parabolas
Let us substitute
So, we get
So, the intersection point P is

Let us find the slope of the tangent to parabola
We know that the slope of the tangent at any point for a conic is defined as
Let us differentiate
So, we get
Now, let us find the slope of the tangent to parabola
Let us differentiate
So, we get
We know that if the two parabolas touch each other at a point, then they will have a common tangent at that point. This means that the slope of both the tangents should be equal.
From equation (1) and (2), we can see that the slopes are equal which means that the parabolas are not touching each other at point P.
We know that if the two parabolas are perpendicular to each other at a point, then they will have a perpendicular tangent at that point. This means that the product of slopes of both the tangents should be equal to ‘–1’.
Let us multiply the slopes obtained in equation (1) and (2). So, we get
Now, let us find the angles made by each tangent with x-axis.
We know that the slope of any line is equal to the tangent of the angle made by a line with x-axis.
Let us assume the angles made by these two tangents with x-axis be
So, we have
And
Let us add the angles
We have
We know that
So, we get
We know that the sum of two complementary angles is
So, the tangents of both the parabolas at point P make complementary angles with x-axis.
So, the correct answer is “Option a”.
Note: We can see that the given problem contains a heavy amount of calculation, so we need to avoid calculation mistakes while solving this problem. We can also find the equation of the tangents at the point of the intersection P using the slope of each of the tangents. We should not consider the value of x which may give origin as the intersection as it is clearly mentioned in the problem. Similarly, we can expect problems to find the sum of the angles made by normal at this point with x-axis.
Recently Updated Pages
The correct geometry and hybridization for XeF4 are class 11 chemistry CBSE

Water softening by Clarks process uses ACalcium bicarbonate class 11 chemistry CBSE

With reference to graphite and diamond which of the class 11 chemistry CBSE

A certain household has consumed 250 units of energy class 11 physics CBSE

The lightest metal known is A beryllium B lithium C class 11 chemistry CBSE

What is the formula mass of the iodine molecule class 11 chemistry CBSE

Trending doubts
Why was the Vernacular Press Act passed by British class 11 social science CBSE

Arrange Water ethanol and phenol in increasing order class 11 chemistry CBSE

Name the nuclear plant located in Uttar Pradesh class 11 social science CBSE

What steps did the French revolutionaries take to create class 11 social science CBSE

How did silk routes link the world Explain with three class 11 social science CBSE

What are the various challenges faced by political class 11 social science CBSE




