Question

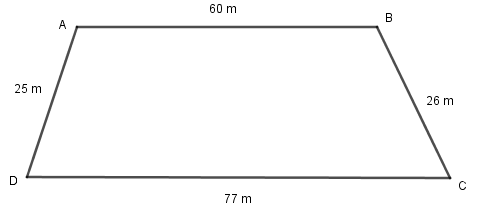
Two parallel sides of a trapezium are 60 m and 77 m and other sides are 25 m and 26 m. Find the area of the trapezium.

Answer 1

Hint: Here, draw BE parallel to AD and draw BF perpendicular to CD. Find the area of the triangle formed using heron’s formula. Using the area obtained, find the height of the triangle or height of trapezium. Now apply the formula of area of trapezium.

Complete step-by-step answer:
Here we are given a trapezium in which all sides are given. Let ABCD be the trapezium of give sides.

Now, draw a line BE parallel to AD. And draw perpendicular line BF on DC.

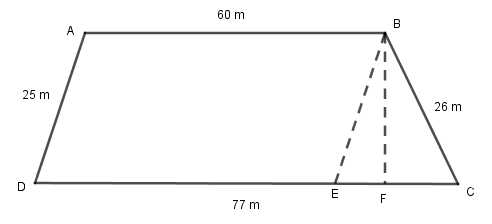
Now, ABED is a parallelogram, in which AB = 60 m, DE = 60 m, AD = 25 m and BE = 25 m. In triangle BEC, BE = 25 m, BC = 26 m and EC = DC – DE = 77 m – 60 m = 17 m.
Finding area of triangle BEC
Sides of triangle BEC, 25 m, 17 m and 26 m
Semi perimeter of triangle BEC, $s = \dfrac{{25 + 17 + 26}}{2} = \dfrac{{68}}{2} = 34{\text{m}}$
Heron’s formula of area of triangle, $A = \sqrt {s(s - a)(s - b)(s - c)} $, where s is semi-perimeter of triangle and a, b, c are sides of the triangle.
Area = $\sqrt {34(34 - 25)(34 - 17)(34 - 26} )$
$ = \sqrt {34 \times 9 \times 17 \times 8} $
$ = \sqrt {17 \times 2 \times 9 \times 17 \times 8} = \sqrt {{{17}^2} \times {4^2} \times {3^2}} = 204$
Area of triangle BEC = 204 sq. m
Also area of triangle BEC = $\dfrac{1}{2} \times EC \times BF$
$ \Rightarrow 204 = \dfrac{1}{2} \times 17 \times BF$
$ \Rightarrow BF = \dfrac{{204 \times 2}}{{17}} = 24$
BF = 24 m i.e height of the triangle is 24 m.
Height of triangle BEC = Height of the trapezium ABCD = 24 m
Area of trapezium = $\dfrac{1}{2}$× (sum of parallel sides) × height
Area of trapezium ABCD = $\dfrac{1}{2}$× (AB + CD) × BF
Area of trapezium ABCD = $\dfrac{1}{2}$× (60 m + 77 m) × 24 m = 137 × 12 sq. m = 1644 sq. m

Area of trapezium is 1644 sq.m

Note: In these types of questions try to find the height of trapezium. In some questions you can divide trapezium into two triangles and find the area of two triangles using heron’s formula and add them to obtain the area of trapezium.