Question

Two poles, $18m$ and $13m$ high, stand upright in the playground. If their feet are $12m$ apart, find the distance between their tops.

Answer 1

Hint: In this question, we are given two poles and the distance between their feet, and we have to find the distance between their tops. For this question, we will first draw a diagram to understand the question better. After that, we will use Pythagoras’ Theorem in the right angles triangle to get the required answer. Pythagoras’ Theorem is given as that the sum of squares of the base and the perpendicular is equal to the square of the hypotenuse, that is, ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$, where $h$ is the hypotenuse, $b$ is the base and $p$ is the perpendicular.

Complete step-by-step solution
Let us first draw a diagram for better understanding.

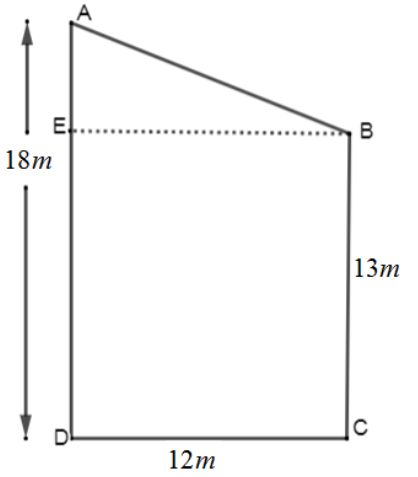
We are given two poles standing upright. So let us take $AD=18m$ and $BC=13m$. Distance between their feet is $12m$, therefore, $DC=12m$. We have to find the distance between their tops, therefore we have to find$AB$.
Since poles are standing upright, therefore $\angle ADC=90{}^\circ $. Let us now draw $BE$ which is parallel to $DC$ and equal to $DC$.
Therefore, $BE=12m$ and $\angle AEB=90{}^\circ $. Hence, we have obtained a right angled triangle $AEB$ with $\angle E=90{}^\circ $ and $BE=12m$.
As we can see from the diagram, $AD=AE+ED$. Since $ED$ is parallel to $BC$ and equal to BC, therefore –
$\begin{align}
  & AD=AE+BC \\
 & 18=AE+13 \\
 & AE=5m \\
\end{align}$
Hence, we now know the value of $AE=5m$.
Now, in right angles triangle $\Delta ABE$,
$AE=5m,BE=12m$ and we have to find the value of $AB$. Using Pythagoras’ theorem, ${{h}^{2}}={{p}^{2}}+{{b}^{2}}$, where $h$ is the hypotenuse, $b$ is the base and $p$ is the perpendicular, we get –
$\begin{align}
  & {{\left( AB \right)}^{2}}={{\left( AE \right)}^{2}}+{{\left( BE \right)}^{2}} \\
 & \Rightarrow {{\left( AB \right)}^{2}}={{\left( 5 \right)}^{2}}+{{\left( 12 \right)}^{2}} \\
 & \Rightarrow {{\left( AB \right)}^{2}}=25+144 \\
 & \Rightarrow {{\left( AB \right)}^{2}}=169 \\
\end{align}$
Taking square root both sides, we get –
$\begin{align}
  & \Rightarrow \left( AB \right)=\sqrt{169} \\
 & \Rightarrow \left( AB \right)=13m \\
\end{align}$
Hence, the distance between their tops is $13m$.

Note: In these types of questions, students should draw diagrams first for a better understanding of the question. Students should not get confused with finding distance between them as their tops are not at the same height, so the distance between their tops can be different between their feet. Pythagoras’ theorem should only be applied in a right-angled triangle.