Question

Two poles of height 6m and 11m stand on a plane ground. If the distance between the feet of the poles is 12m, find the distance between their tops.

Answer 1

Hint: Draw the figure to observe the data given in the question. Use Pythagoras Theorem of right angled triangles to relate the base and perpendicular of the poles. Consider the fact that the pole is perpendicular to the base.

Complete step-by-step answer:
We have two poles of height 6m and 11m which stand on a plane ground such that the distance between their feet is 12m. We have to find the distance between their tops.
Let us assume that the ends of pole of height 6m are A and B and of pole of height 11m are C and D, as shown in the figure.

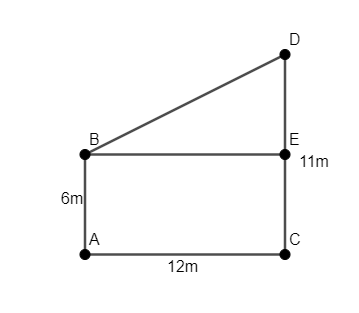
We have to find the length of BD.
We observe that \[AB\bot AC\] and \[CD\bot AC\]. Thus, BE is parallel to AC.
Thus, we observe that ABCD is a rectangle whose opposite sides are equal.
We will find the length of DE.
As ABCD is a rectangle, we have \[AB=CE=6m\].
So, we have \[CD=CE+DE\].
We know that \[CD=11m,CE=6m\].
Thus, we have \[11=6+DE\Rightarrow DE=11-6=5m\].
As ABCD is a rectangle, we have \[AC=BE=12m\].
Now, we will consider the triangle \[\vartriangle BDE\]. We know that \[BE\bot DE\]. Thus, \[\vartriangle BDE\] is a right angled triangle right angled at E.
We will now use Pythagoras Theorem in this triangle. Thus, we have \[{{\left( BE \right)}^{2}}+{{\left( ED \right)}^{2}}={{\left( BD \right)}^{2}}\].
We know that \[BE=12m,DE=5m\].
Thus, we have \[{{\left( BD \right)}^{2}}={{\left( 12 \right)}^{2}}+{{5}^{2}}=144+25=169={{\left( 13 \right)}^{2}}\].
So, we have \[BD=13m\].
Hence, the distance between the top of the poles is \[BD=13m\].

Note: It’s necessary to observe that ABCD is a rectangle and thus, BDE is a right angled triangle. We can’t solve this question without proving that BDE is a right angles triangle. Also, one must know the Pythagoras Theorem of right angled triangles. One should also be careful about the units of length while performing calculations.