Question

Two ships are approaching a light house from opposite directions. The angles of depression of two ships from top of the light house are \[30^\circ \] and \[45^\circ \]. If the distance between two ships is 100m, find the height of the light house.

Answer 1

Hint: Here we will use the trigonometric functions to find the height of the light house. Firstly we will assume the length of a boat from the bottom of the light house. Then by using the trigonometric function we will find the relation between the height of the light house and the distance between the base of the light house and the boat.

Complete step-by-step answer:
Let \[h\] be the height of the light house, \[x\] be the distance of the ship making angle of \[45^\circ \] from the base of the light house.
It is given that the distance between two ships is 100m. Therefore the distance between the ship making an angle of \[30^\circ \]with the light house to the base of the light house will be \[100 - x\].

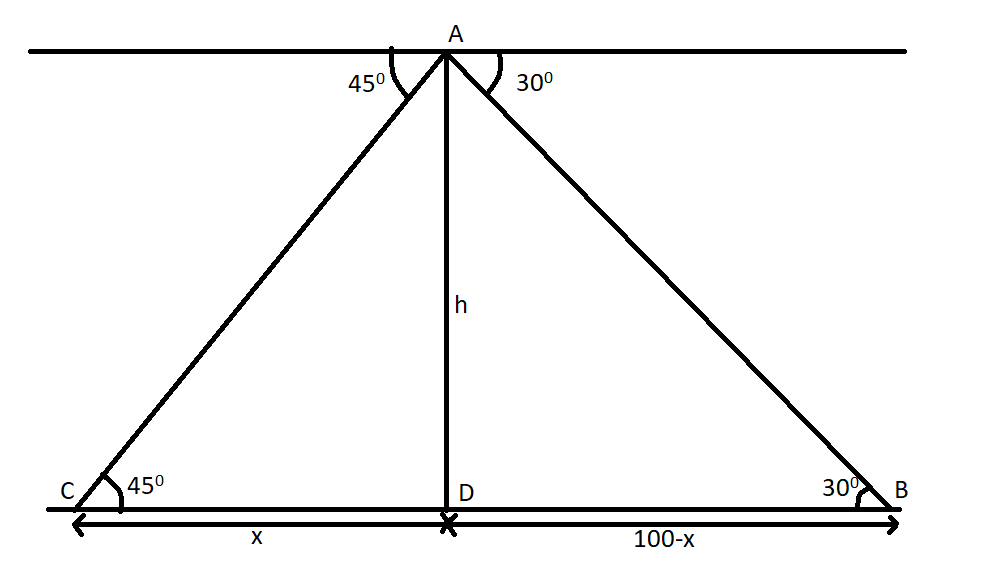
In \[\Delta ACD\], we will use the trigonometric function to get the relation between \[x\] and \[h\]. Therefore we get
\[\tan 45^\circ = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}} = \dfrac{h}{x}\]
We know that \[\tan 45^\circ \] is equal to 1. Therefore, we get
\[ \Rightarrow 1 = \dfrac{h}{x}\]
\[ \Rightarrow h = x\]……………….\[\left( 1 \right)\]
Now we will take the triangle \[\Delta ABD\] and use the trigonometric function to get the relation between \[x\] and \[h\]. Therefore, we get
\[\tan 30^\circ = \dfrac{{{\rm{perpendicular}}}}{{{\rm{base}}}} = \dfrac{h}{{100 - x}}\]
We know that \[\tan 30^\circ \] is equal to \[\dfrac{1}{{\sqrt 3 }}\]. Therefore, we get
\[ \Rightarrow \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{{100 - x}}\]
\[ \Rightarrow \sqrt 3 h = 100 - x\]
Now, substituting the value of \[h\] from the equation \[\left( 1 \right)\] in the above equation, we get
\[ \Rightarrow \sqrt 3 h = 100 - h\]
\[ \Rightarrow \sqrt 3 h + h = 100\]
\[ \Rightarrow h = \dfrac{{100}}{{1 + \sqrt 3 }} = 36.6m\]
Hence, the height of the light house is equal to \[36.6m\].

Note: Here we should note that in these types of questions, where the height of some tower or poles is asked to find, then we have to use the trigonometric function to find its value. Also any building or tower constructed on the ground is generally perpendicular to the ground this is why we can use the trigonometric function to find the value of its height.