Question

Two small magnets $A$ and $B$ of dipole moments \[{M_0}\] and \[2{M_0}\] respectively are fixed perpendicular to each other with their North poles in contact. The combination is placed on a floating body so as to move freely in earth's magnetic field ( Shown \[{B_H}\] in figure ), the value of \[\alpha \] is :

A. \[{\tan ^{ - 1}}(2)\]
B. \[{\sin ^{ - 1}}(\dfrac{1}{2})\]
C. \[{\cos ^{ - 1}}(\dfrac{1}{2})\]
D. none of these

Answer 1

Hint: Newton’s second law of motion states that any object will be at rest if the net force acting on it is zero. The two magnetic dipoles will be at equilibrium when the sine component of the dipole will be equal to each other.

Formula used:
The torque on a dipole placed in a magnetic field is given by,
\[\tau = MB\operatorname{Sin} \theta \]
where \[\tau \] is the torque on the dipole, \[M\] is the dipole moment of the dipole, \[B\] is the external magnetic field applied to it and \[\theta \] is the angle between the magnetic field and the dipole.

Complete step by step answer:
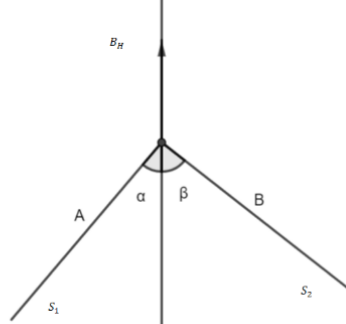
We have given here to small magnets which are placed perpendicular to each other with the north pole in contact between them. Now the dipoles will be at rest if the net force acting on the system is zero.Now, the force acting on it is the torque due to the earth’s magnetic field.So, these torques will be equal to each other for the dipoles to be at rest. We know that, the torque acting on a particle dipole in a magnetic field is given by,
\[\tau = MB\operatorname{Sin} \theta \]
where \[\tau \] is the torque on the dipole,\[M\] is the dipole moment of the dipole, \[B\] is the external magnetic field applied to it and \[\theta \] is the angle between the magnetic field and the dipole.

So, the torque acting on the first dipole is,
\[{\tau _1} = {M_0}{B_H}\operatorname{Sin} \alpha \\ \]
And the torque acting on the first dipole is,
\[{\tau _2} = 2{M_0}{B_H}\operatorname{Sin} \beta \\ \]
Now, to be at equilibrium these torques will be equal. Hence, we can write,
\[{M_0}{B_H}\operatorname{Sin} \alpha = 2{M_0}{B_H}\operatorname{Sin} \beta \\ \]
Now, given here, \[\alpha + \beta = {90^ \circ }\]
Hence, we can write,
\[{M_0}{B_H}\operatorname{Sin} \alpha = 2{M_0}{B_H}\operatorname{Sin} ({90^ \circ } - \alpha )\]
\[\Rightarrow\operatorname{Sin} \alpha = 2\cos \alpha \]
\[\Rightarrow \tan \alpha = 2\]
\[\therefore \alpha = {\tan ^{ - 1}}(2)\]
Hence, the value of the angle \[\alpha \] is \[{\tan ^{ - 1}}(2)\].

Hence, option A is the correct answer.

Note: When the dipoles are connected by the North Pole the force applied by the earth’s magnetic keeps it in place though the poles repulse each other. To solve this type of problem when the system is at equilibrium always remember that the net force acting on equilibrium is zero.