Question

Two towns A and B are connected by a regular bus service with a bus leaving in either direction every T minutes. A man cycling with a speed of 20 km/h in the direction A to B notices that a bus goes post him every 18 minutes in the direction of his motion, and every 6 minutes in the opposite direction. What is the period T of the bus service and with what speed do the buses ply on the road?

Answer 1

Hint: In this problem, you have to be very conceptual, otherwise it is very confusing. We will just imagine a timeline and place the incidents there as necessary to solve the problem. BY considering various activities like “in the direction of motion”, “opposite of direction of motion”.

Formula used: $$ d=v \times t $$

Complete step by step solution:
Let us take the velocity of the bus to be v. Also, for our convenience, let the person and a bus start at time $t_1$ o’clock from town A. And let another bus and the person reach town B at time $t_2$ o’clock.

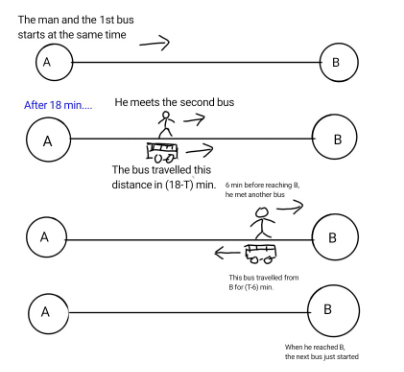
In the direction of motion:

The man meets another bus at time $t_1+18$ min. By the time, he has covered the distance of $d_1=\dfrac{20 km}{60 min}\times 18 min= 6km $. The next bus started at, $t_1+T$ min. So, the next bus has travelled this 6 km in $((t_1+18)-(t_1+T))=18-T$ min. So ….

$(18-T).v=6 …………………1^{st}$ equation

Opposite to the direction of motion:

The man and the bus reach town B at $t_2$ . He met the previous bus at $t_2-6$ min when he was $d_2=\dfrac{20 km}{60 min} \times 6 min=2km $ . And the previous bus started from B at $t_2-T$ . So, the previous bus travelled 2 km in time $((t_2-6)-(t_2-T))=T-6$ min. So …..
$(T-6).v=2 ……………………..2^{nd}$ equation

Solving two equations, we get

T= 9 min and $v=\dfrac{2}{3} km/min=\dfrac{2\times 60}{3} km/h=40 km/h $

This is the required answer.

Additional information:
When two objects move in the same direction, the relative velocity is the difference of their velocities. If they move in opposite directions, relative velocity is the addition of their velocities. However, this concept has not been used here.

Note: Notice that we have made the calculation taking velocity in units of km/min. Later, we have converted the answer into km/h. Try to have a clear idea about the timeline to understand this problem. Students often forget to convert all the units in one single value.