Question

Two triangles having the same base (or equal base) and equal areas lie between the same parallels.

Answer 1

Hint:
Here, we have to prove that the two triangles having the same base (or equal base) and equal areas lie between the same parallels. Two triangles having the same base should lie in a parallelogram.

Formula used:
We will use the formula of area of the triangle = \[\dfrac{1}{2} \times b \times h\] sq. units where \[b\] is the base of the triangle and \[h\] is the height of the triangle.

Complete step by step solution:
Two triangles \[ABC\] and \[ABD\] lie on the same base \[AB\] such that \[Area(\Delta ABC) = Area(\Delta ABD)\] lie between the same parallels. We can draw the altitudes of \[\Delta ABC\] and \[\Delta ABD\] through \[C\] and \[D\] and meet the bases \[AB\] at \[E\] and \[F\] respectively.

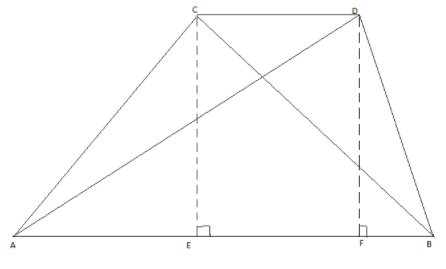
Now, we have to prove \[CD \bot AB\] .
Since \[CE\] and \[DF\] are perpendicular to \[AB\], \[CE\] and \[DF\]are parallel to each other.
Since lines perpendicular to the same line are parallel to each other.
$\therefore CE\bot DF$ .
Now, we are given that \[Area(\Delta ABC) = Area(\Delta ABD)\].
\[Area(\Delta ABC) = \dfrac{1}{2} \times b \times h = \dfrac{1}{2} \times AB \times CE\]
\[Area(\Delta ABD) = \dfrac{1}{2} \times b \times h = \dfrac{1}{2} \times AB \times DF\]
Since, \[Area(\Delta ABC) = Area(\Delta ABD)\]
\[ \Rightarrow \dfrac{1}{2} \times AB \times CE = \dfrac{1}{2} \times AB \times DF\]
\[ \Rightarrow CE = DF\]
Now, in CDFE, we have
\[ \Rightarrow CE = DF\] and \[CE \bot DF\]
Since, a pair of opposite sides are parallel and equal,
Hence, \[CDFE\] is a parallelogram.
We know that Opposite sides of parallelograms are parallel.
So that \[CD \bot EF\]
Since, \[EF\] lies on the plane \[AB\] , we have
\[ \Rightarrow CD \bot AB\] . Hence proved.

Therefore, two triangles having the same base (or equal base) and equal areas lie between the same parallels.

Note:
We know that if two triangles are equal, they are congruent to each other. It is not necessary that two triangles with the same base have the same area. But their altitudes should be the same as well, for the triangle to be with equal area. Two triangles on the same base between the same parallel lines are equal in area.