Question

Two waves in the same medium are represented by $y-t$ curves in the figure shown. Find the ratio of their average intensities.

$\begin{align}
  & (A)\dfrac{25}{16} \\
 & (B)\dfrac{23}{16} \\
 & (C)\dfrac{21}{16} \\
 & (D)\dfrac{27}{16} \\
\end{align}$

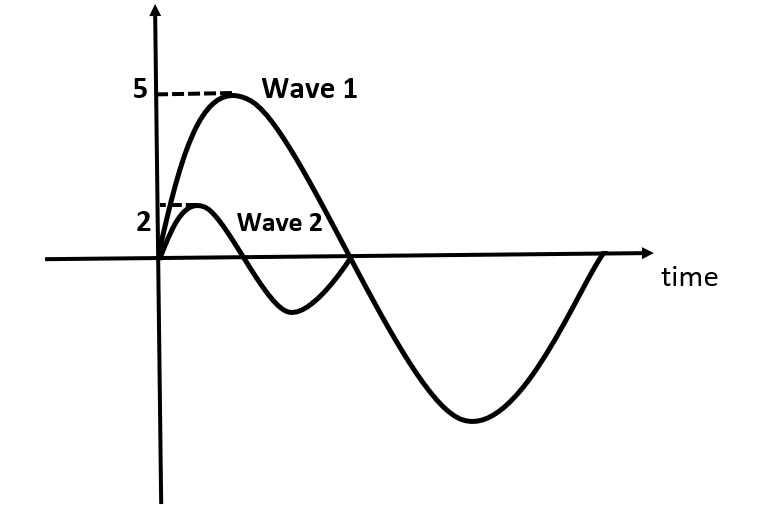
Answer 1

Hint: We have the graphical representation of two waves. From the graph, we can determine the Amplitude of the two sinusoidal waves. Once the amplitude of these waves are known, we can calculate the ratio of intensities of the two waves. This can be calculated using the fact that the intensity of any wave is proportional to the square of its amplitude. We will proceed in the above aforesaid manner.

Complete answer:
Let the amplitude of the larger wave be ${{A}_{1}}$ and the amplitude of the smaller wave be ${{A}_{2}}$. Then, from the given graphical diagram, we can say that:
$\Rightarrow {{A}_{1}}=5$ And,
$\Rightarrow {{A}_{2}}=2$
Now, the relation between intensity and amplitude of a wave is given by:
$\begin{align}
  & \Rightarrow I\propto {{(A\omega )}^{2}} \\
 & \Rightarrow I\propto {{(Af)}^{2}} \\
\end{align}$
Where f is the frequency of the wave.
This could be written as:
$\Rightarrow \dfrac{I}{{{(Af)}^{2}}}=k$
Where, k is an arbitrary constant called the constant of proportionality.
Therefore, for two waves in comparison. We can write as follows:
$\Rightarrow \dfrac{{{I}_{1}}}{{{A}_{1}}^{2}{{f}_{1}}^{2}}=\dfrac{{{I}_{2}}}{{{A}_{2}}^{2}{{f}_{2}}^{2}}$
On rearranging terms, we get:
$\Rightarrow \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{A}_{1}}^{2}{{f}_{1}}^{2}}{{{A}_{2}}^{2}{{f}_{2}}^{2}}$
Putting the values of both the amplitudes in the above equation and simplifying the equation, we get:
$\begin{align}
  & \Rightarrow \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{{{\left( 5 \right)}^{2}}{{\left( 1 \right)}^{2}}}{{{\left( 2 \right)}^{2}}{{\left( 2 \right)}^{2}}} \\
 & \therefore \dfrac{{{I}_{1}}}{{{I}_{2}}}=\dfrac{25}{16} \\
\end{align}$
Hence, the ratio of their average intensities of the two waves, comes out to be $\dfrac{25}{16}$.

Hence, option (A) is the correct option.

Note:
Here, the ratio of intensity would have been equal to the ratio of amplitude squared only, if the frequency of both the waves would have been the same. But that wasn’t the case, so we included an extra term, the angular frequency which is directly proportional to frequency into our equation to avoid mistakes. One should also be careful in writing the correct ratio in answer.