Question

How do you use the integral test to determine if $\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{9}+\dfrac{1}{11}.......$ is convergent or divergent?

Answer 1

Hint: We can solve this question by drawing the graph of $\dfrac{1}{2x+1}$ . We can prove some series is divergent if some less value than the series is divergent. We can prove some series convergent if some greater value than the series is convergent.

Complete step by step answer:
In the series $\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{9}+\dfrac{1}{11}.......$ we can see the denominators are 3,5,7….
We can write the series $\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{9}+\dfrac{1}{11}.......=\sum\limits_{n=1}^{\infty }{\dfrac{1}{2n+1}}$
Let’s the graph of $\dfrac{1}{2x+1}$
  

Lets mark the area under the curve when $1\le x<\infty $

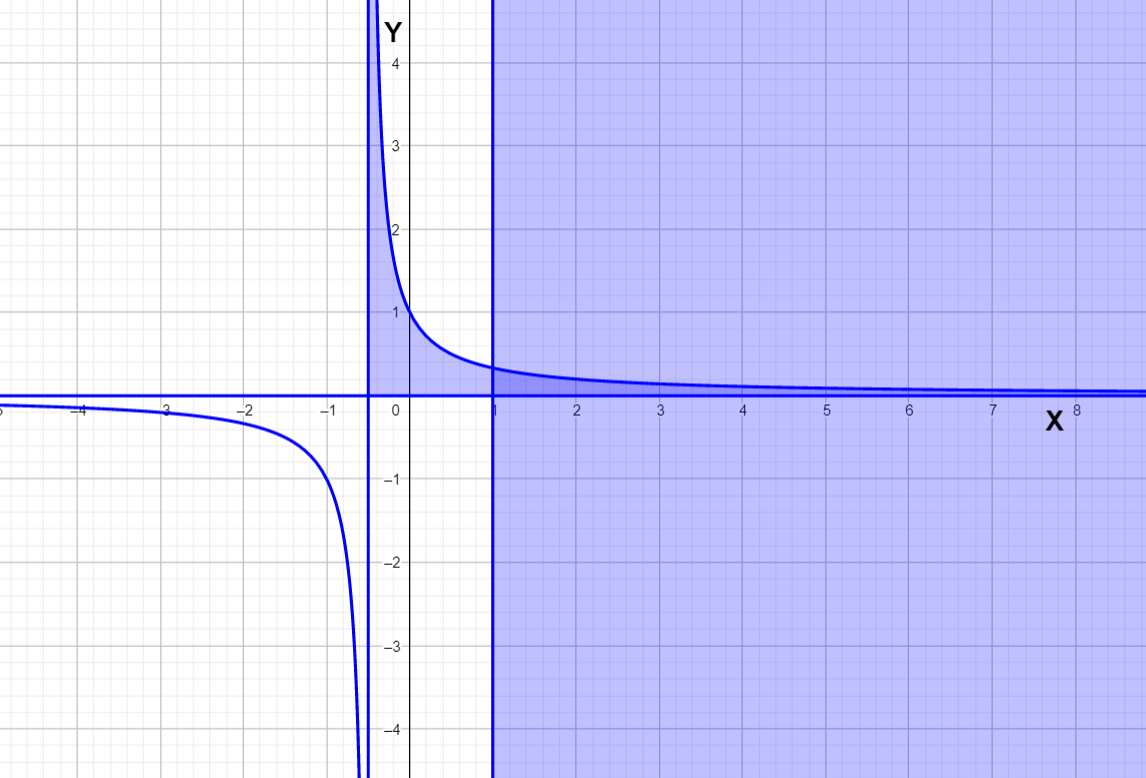
The region with deep blue color is our required area we can calculate the area by integrating
$\dfrac{1}{2x+1}$
From 1 to infinity
So the area under the curve =$\int\limits_{1}^{\infty }{\dfrac{1}{2x+1}dx}$
$=\left[ \dfrac{1}{2}\ln \left( 2x+1 \right) \right]_{1}^{\infty }$
We know that logarithm is tend to infinity when x tends to infinity
So the area under the curve tends to infinity.
Now let’s look at the series given in the question $\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{9}+\dfrac{1}{11}.......$
If can write the series as
$\dfrac{1}{3}\times 1+\dfrac{1}{5}\times 1+\dfrac{1}{7}\times 1..........$
We represent the series in as area in a Cartesian plane and compare with above area under the curve

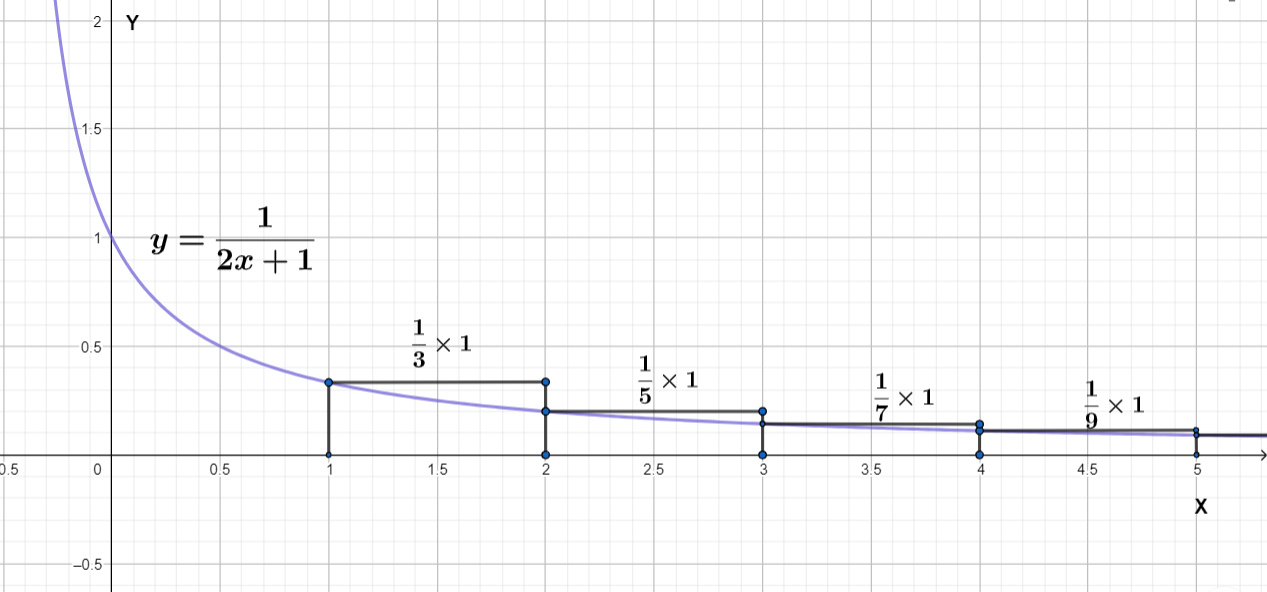
All the rectangle represents the area
$\dfrac{1}{3}\times 1+\dfrac{1}{5}\times 1+\dfrac{1}{7}\times 1..........$
We can clearly see the sum of the area of all rectangles is greater than the area under the curve from 1 to infinity.
If the area under the curve tends to infinity then the area of all rectangles will automatically tend to infinity.
So the sum of the series
$\dfrac{1}{3}+\dfrac{1}{5}+\dfrac{1}{7}+\dfrac{1}{9}+\dfrac{1}{11}.......$
Will tend to infinity. So the series is divergent.

Note:
If nth term of a series is a nonzero number when n tends to infinity then the series is definitely divergent but the reverse is not true that means if nth term tends to 0 when n tends to infinity that does not mean the series will be convergent like we have seen in the above example. In the above series the nth term tends to 0 when n tends to infinity but the series
Is divergent.