How do you use the law of cosines to find the area of a triangle?
Answer
Verified538.2k+ views
Hint: Here, we will first draw the diagram of a triangle and apply the law of cosine on any one of the angles. Then we will use the sine and cosine ratios in the right-angled triangle to find the height of the triangle. Then we will apply the Pythagoras theorem to find the base of the triangle. We will then substitute these values in the formula of the area of the triangle to get the required area.
Formula Used:
We will use the following formulas:
1. The law of cosines states that \[{c^2} = {a^2} + {b^2} - 2ab\cos C\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[C\] is the angle opposite to the side of length \[c\].
2. \[\sin x = \dfrac{P}{H}\]
3. \[\cos x = \dfrac{B}{H}\]
4. The area of a triangle is given by the formula \[\Delta = \dfrac{1}{2}ab\sin C\], where \[a\] is the length of the side opposite to angle \[A\], and \[b\] is the length of the side opposite to angle \[B\].
Complete step-by-step solution:
We will use the law of cosines to find the area of a triangle.
First, we will draw a triangle ABC with height AD.
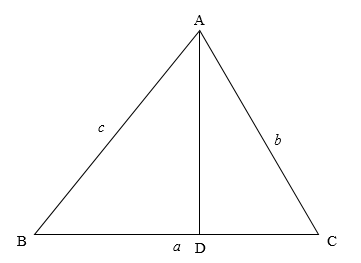
The law of cosines states that \[{c^2} = {a^2} + {b^2} - 2ab\cos C\].
Rewriting the equation, we get
\[ \Rightarrow 2ab\cos C = {a^2} + {b^2} - {c^2}\]
Dividing both sides of the equation by \[2ab\], we get
\[ \Rightarrow \cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\]
The sine of an angle of a right-angled triangle is the ratio of its perpendicular and hypotenuse.
This can be written as \[\sin x = \dfrac{P}{H}\].
Therefore, in triangle ADC, we get
\[\sin C = \dfrac{{AD}}{{AC}}\]
Substituting \[b\] for AC in the equation, we get
\[ \Rightarrow \sin C = \dfrac{{AD}}{b}\]
Thus, we get the height of the triangle as
\[ \Rightarrow AD = b\sin C\]
The cosine of an angle of a right angled triangle is the ratio of its base and hypotenuse.
This can be written as \[\cos x = \dfrac{B}{H}\].
Therefore, in triangle ADC, we get
\[\cos C = \dfrac{{DC}}{{AC}}\]
Substituting \[b\] for AC in the equation, we get
\[ \Rightarrow \cos C = \dfrac{{DC}}{b}\]
Thus, we get the height of the triangle as
\[ \Rightarrow DC = b\cos C\]
Now, we will use the Pythagoras theorem in triangle ADC.
Using the Pythagoras theorem in triangle ADC, we get
\[A{C^2} = A{D^2} + C{D^2}\]
Substituting \[AC = b\], \[AD = b\sin C\], and \[DC = b\cos C\] in the equation, we get
\[ \Rightarrow {b^2} = {\left( {b\sin C} \right)^2} + {\left( {b\cos C} \right)^2}\]
Rewriting the equation, we get
\[ \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left( {b\cos C} \right)^2}\]
Substituting \[\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\] in the equation, we get
\[ \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left[ {b\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}} \right)} \right]^2}\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)^2}\\ \Rightarrow b\sin C = \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \end{array}\]
The area of a triangle can be calculated using two sides and the angle between them, using the formula \[\Delta = \dfrac{1}{2}ab\sin C\].
Substituting \[b\sin C = \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \] in the formula for area of triangle, we get
\[\Delta = \dfrac{1}{2}a \times \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \]
Simplifying the equation, we get
\[ \Rightarrow \Delta = \dfrac{{a\sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} }}{2}\]
Therefore, the area of the triangle using law of cosines can be found using the formula \[\dfrac{{a\sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} }}{2}\].
Note:
We used Pythagoras’s theorem in the triangle ABC. The Pythagoras’s theorem states that the square of the hypotenuse of a right-angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}\]. The hypotenuse of a right-angled triangle is its longest side.
We can also use the law of cosines with Heron's formula to find the area of a triangle. The law of cosines is used when the lengths of two sides and the angle between them is given. Using the law of cosines, the length of the third side can be calculated. Using the lengths of the three sides, we can apply Heron’s formula and obtain the area of the triangle.
Formula Used:
We will use the following formulas:
1. The law of cosines states that \[{c^2} = {a^2} + {b^2} - 2ab\cos C\], where \[a\], \[b\], and \[c\] are the lengths of the sides of the triangle, and \[C\] is the angle opposite to the side of length \[c\].
2. \[\sin x = \dfrac{P}{H}\]
3. \[\cos x = \dfrac{B}{H}\]
4. The area of a triangle is given by the formula \[\Delta = \dfrac{1}{2}ab\sin C\], where \[a\] is the length of the side opposite to angle \[A\], and \[b\] is the length of the side opposite to angle \[B\].
Complete step-by-step solution:
We will use the law of cosines to find the area of a triangle.
First, we will draw a triangle ABC with height AD.
The law of cosines states that \[{c^2} = {a^2} + {b^2} - 2ab\cos C\].
Rewriting the equation, we get
\[ \Rightarrow 2ab\cos C = {a^2} + {b^2} - {c^2}\]
Dividing both sides of the equation by \[2ab\], we get
\[ \Rightarrow \cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\]
The sine of an angle of a right-angled triangle is the ratio of its perpendicular and hypotenuse.
This can be written as \[\sin x = \dfrac{P}{H}\].
Therefore, in triangle ADC, we get
\[\sin C = \dfrac{{AD}}{{AC}}\]
Substituting \[b\] for AC in the equation, we get
\[ \Rightarrow \sin C = \dfrac{{AD}}{b}\]
Thus, we get the height of the triangle as
\[ \Rightarrow AD = b\sin C\]
The cosine of an angle of a right angled triangle is the ratio of its base and hypotenuse.
This can be written as \[\cos x = \dfrac{B}{H}\].
Therefore, in triangle ADC, we get
\[\cos C = \dfrac{{DC}}{{AC}}\]
Substituting \[b\] for AC in the equation, we get
\[ \Rightarrow \cos C = \dfrac{{DC}}{b}\]
Thus, we get the height of the triangle as
\[ \Rightarrow DC = b\cos C\]
Now, we will use the Pythagoras theorem in triangle ADC.
Using the Pythagoras theorem in triangle ADC, we get
\[A{C^2} = A{D^2} + C{D^2}\]
Substituting \[AC = b\], \[AD = b\sin C\], and \[DC = b\cos C\] in the equation, we get
\[ \Rightarrow {b^2} = {\left( {b\sin C} \right)^2} + {\left( {b\cos C} \right)^2}\]
Rewriting the equation, we get
\[ \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left( {b\cos C} \right)^2}\]
Substituting \[\cos C = \dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}\] in the equation, we get
\[ \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left[ {b\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2ab}}} \right)} \right]^2}\]
Simplifying the equation, we get
\[\begin{array}{l} \Rightarrow {\left( {b\sin C} \right)^2} = {b^2} - {\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)^2}\\ \Rightarrow b\sin C = \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \end{array}\]
The area of a triangle can be calculated using two sides and the angle between them, using the formula \[\Delta = \dfrac{1}{2}ab\sin C\].
Substituting \[b\sin C = \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \] in the formula for area of triangle, we get
\[\Delta = \dfrac{1}{2}a \times \sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} \]
Simplifying the equation, we get
\[ \Rightarrow \Delta = \dfrac{{a\sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} }}{2}\]
Therefore, the area of the triangle using law of cosines can be found using the formula \[\dfrac{{a\sqrt {{b^2} - {{\left( {\dfrac{{{a^2} + {b^2} - {c^2}}}{{2a}}} \right)}^2}} }}{2}\].
Note:
We used Pythagoras’s theorem in the triangle ABC. The Pythagoras’s theorem states that the square of the hypotenuse of a right-angled triangle is equal to the sum of squares of the other two sides, that is \[{\rm{Hypotenus}}{{\rm{e}}^2} = {\rm{Bas}}{{\rm{e}}^2} + {\rm{Perpendicula}}{{\rm{r}}^2}\]. The hypotenuse of a right-angled triangle is its longest side.
We can also use the law of cosines with Heron's formula to find the area of a triangle. The law of cosines is used when the lengths of two sides and the angle between them is given. Using the law of cosines, the length of the third side can be calculated. Using the lengths of the three sides, we can apply Heron’s formula and obtain the area of the triangle.
Recently Updated Pages
Trending doubts
What is meant by exothermic and endothermic reactions class 11 chemistry CBSE
10 examples of friction in our daily life
One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE
1 Quintal is equal to a 110 kg b 10 kg c 100kg d 1000 class 11 physics CBSE
Difference Between Prokaryotic Cells and Eukaryotic Cells
The camels hump is made of which tissues a Skeletal class 11 biology CBSE