Question

Use Venn diagrams to verify De Morgan’s law for set difference $A/\left( B\cap C \right)=\left( A/B \right)\cup \left( A/C \right).$

Answer 1

Hint: $X\cap Y$ means elements common to set x and set y. $X\cup Y$ means all the elements belong to set x or set y. x/y means all the elements of x not lying in y. represent the left hand side of the given equation in a venn diagram and compare it with the venn diagram of right hand side of the equation. Use the above mentioned concepts to draw the accurate venn diagram.
Complete step-by-step answer:
Here, we have to verify the relation $A/\left( B\cap C \right)=\left( A/B \right)\cup \left( A/C \right)$ with the help of Venn diagrams. So, we have to prove
$A/\left( B\cap C \right)=\left( A/B \right)\cup \left( A/C \right)$……………. (i)
Let us represent the Venn diagrams of both the sides of the equation individually and then try to relate the connection between them.
So, let us represent $A/\left( B\cap C \right)$ by taking 3 sets A, B, C.
Hence, A, B, C sets can be represented as

Here, we supposed the number of variables for the different parts of the Venn diagram. It means a, b, c, d, e, f, g are the number of elements to that part of the Venn diagram.
So, we have to draw a Venn diagram for $A/\left( B\cap C \right)$.
$B\cap C$ will be the region which contains elements of both the sets B, C.
Now, from the diagram the number of elements in $B\cap C$ is d + e, it can be represented as:

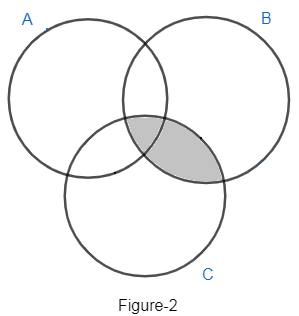
Now we need to find $A/\left( B\cap C \right)$. It means $B\cap C$ region is given, we need to find the elements of A which do not belong to $B\cap C$ region. So, the number of elements is given as
a + b + c. it can be represented as

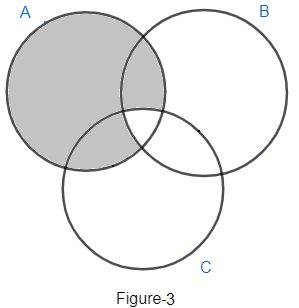
Now, we need to represent the expression on the right hand side of equation (i). The expression is given as $\left( A/B \right)\cap \left( A/C \right)$ ……………..(ii)
Let us represent A/B. It means the elements of A not lying in B. So, the number of elements from figure 1 is given as a + c. So, Venn diagram of A/B can be given as

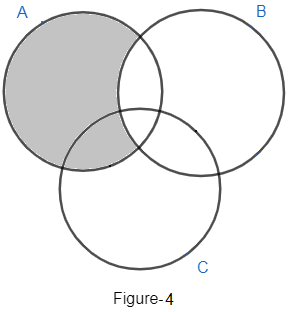
Similarly, A/C will consist of elements of A, which are not lying in C. So, we get the number of elements in A/C as a + b. Venn diagram of A/C is given as

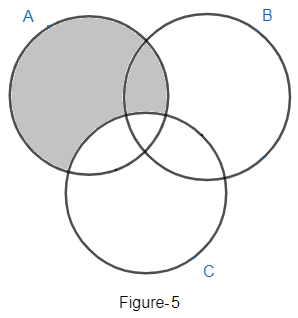
Now, we can draw Venn diagram of $\left( A/B \right)\cup \left( A/C \right)$ by taking all the elements of A/B, A/C. so, number of elements in $\left( A/B \right)\cup \left( A/C \right)$ can be given as a + b + c and Venn diagram can be represented as

Now, we can compare the figure 3 of representation of $A/\left( B\cap C \right)$ and figure 6 of representation of $\left( A/B \right)\cup \left( A/C \right)$. So, both are the same and the number of elements in both the diagrams are a + b + c elements from figure 1.
Hence, $A/\left( B\cap C \right)\left( A/B \right)\cup \left( A/C \right)$ is proved.
Note: One may get confused with the relation A/B and may take elements of B which are not lying A, i.e. just opposite of the exact definition of A/B; which is wrong and students always get confuse with the definition of A/B. so, be clear with the representation A/B.
Draw the Venn diagram very accurately and try to get the region of the expression at each step of the solution to get the accurate answer. One may miss any part of the region and hence, will get the wrong results. So, take care with it as well.