Question

Using integration, find the area of the triangle whose vertices are A(1, 3), B(2, 5) and C(3, 4).

Answer 1

Hint: Geometrically, definite integration can be used to find the area under the given curve up to the x-axis. We will first find the equation of the sides AB, BC and AC of the triangle. The imaginary line through B, which divides the figure in two parts will be used as reference. The sum of the area under AB and BC will give the total area between the lines and the x-axis. We have to subtract the area below the triangular region to find the net area inside the triangle. This can be done by subtracting the area under line AC. The enclosing area is found using the formula-

$\mathop \smallint \nolimits_{{\text{x}} = {\text{a}}}^{{\text{x}} = {\text{b}}} {\text{f}}\left( {\text{x}} \right)d{\text{x}} = area$

Complete step-by-step answer:

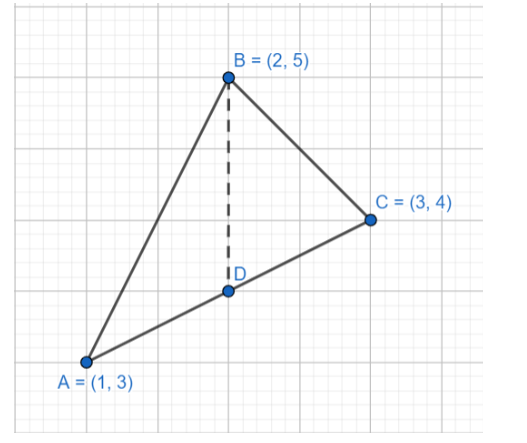
Using the two point form, the equation of the straight line is-
${\text{y}} - {{\text{y}}_1} = \dfrac{{{{\text{y}}_2} - {{\text{y}}_1}}}{{{{\text{x}}_2} - {{\text{x}}_1}}}\left( {{\text{x}} - {{\text{x}}_1}} \right)$
For line AB,
${\text{y}} - 3 = \dfrac{{5 - 3}}{{2 - 1}}\left( {{\text{x}} - 1} \right)$
${\text{y}} - 3 = 2{\text{x}} - 2$
${\text{y}} = 2{\text{x}} + 1...\left( 1 \right)$
For line BC,
${\text{y}} - 5 = \dfrac{{4 - 5}}{{3 - 2}}\left( {{\text{x}} - 2} \right)$
${\text{y}} - 5 = - {\text{x}} + 2$
${\text{y}} = - {\text{x}} + 7...\left( 2 \right)$
For line CA,
$y - 4 = \dfrac{{3 - 4}}{{1 - 3}}\left( {x - 3} \right)$
$y - 4 = \dfrac{1}{2}x - \dfrac{3}{2}$
$y = \dfrac{1}{2}x + \dfrac{5}{2}...\left( 3 \right)$
We will divide the triangle into two parts using the line x = 2, as shown in the figure. The first part inside the triangle can be calculated by finding the area under the line AB, and then subtracting the region below the triangle, which is the area under the line AD. Similarly, the second part is an area with a difference of area under lines BC and DC.
So, for the first portion-

Area I = area under AB - area under AD
$ = \mathop \smallint \nolimits_1^2 \left( {2{\text{x}} + 1} \right)d{\text{x}} - \mathop \smallint \nolimits_1^2 \left( {\dfrac{1}{2}{\text{x}} + \dfrac{5}{2}} \right)d{\text{x}}$
$ = \left( {{{\text{x}}^2} + {\text{x}}} \right)_1^2\; - \;\left( {\dfrac{{{{\text{x}}^2}}}{4} + \dfrac{5}{2}{\text{x}}} \right)_1^2$
$ = \left[ {4 + 2 - \left( {1 + 1} \right)} \right] - \left[ {\dfrac{4}{4} + \dfrac{{10}}{2} - \left( {\dfrac{1}{4} + \dfrac{5}{2}} \right)} \right]$
$ = 4 - \left[ {1 + 5 - \dfrac{{11}}{4}} \right]$
$ = - 2 + \dfrac{{11}}{4} = \dfrac{3}{4}$
For the second portion-
Area II = area under BC - area under DC
$ = \mathop \smallint \nolimits_2^3 \left( { - x + 7} \right)d{\text{x}} - \mathop \smallint \nolimits_2^3 \left( {\dfrac{1}{2}{\text{x}} + \dfrac{5}{2}} \right)d{\text{x}}$
$ = \left( { - \dfrac{{{{\text{x}}^2}}}{2} + 7{\text{x}}} \right)_2^3 - \left( {\dfrac{{{{\text{x}}^2}}}{4} + \dfrac{5}{2}{\text{x}}} \right)_2^3$
$ = \left[ { - \dfrac{9}{2} + 21 - \left( { - \dfrac{4}{2} + 14} \right)} \right] - \left[ {\dfrac{9}{4} + \dfrac{{15}}{2} - \left( {\dfrac{4}{4} + \dfrac{{10}}{2}} \right)} \right]$
$ = \left[ { - \dfrac{9}{2} + 21 + 2 - 14} \right] - \left[ {\dfrac{9}{4} + \dfrac{{15}}{2} - 1 - 5} \right]$
$ = \dfrac{9}{2} - \dfrac{{15}}{4} = \dfrac{3}{4}$
Area of the triangle is given by-
Area I + Area II =
$\dfrac{3}{4} + \dfrac{3}{4} = \dfrac{3}{2}\;sq\;units$
This is the required answer.

Note: In such types of questions, we may need to divide the figure into two or more regions as shown in the figure. Also, a diagram is necessary to solve the problem correctly. Alternatively, we can use y-axis as the reference and then find the area of the triangle. A common mistake is that sometimes the area under the graph comes out to be negative, and the students leave it as it is. To prevent this, they should use the modulus sign, because the area of any region cannot be negative.