Question

Using ruler and compass only, construct a triangle ABC, having AB = 47 cm, AC = 34 cm and $\angle BAC={{75}^{0}}$ . Draw the perpendicular bisector of BC and the bisector of the angle BAC. If the perpendicular bisector and the angle bisector meet at a point M, measure $\angle BMC$ .

Answer 1

Hint: For solving this question first we will see how to draw an angle of ${{75}^{0}}$ and bisect it, and how to draw perpendicular bisector of any line segment. After that, we will proceed stepwise as per the data given in the problem and know how to draw angles and lines using ruler and compass.

Complete step by step solution:
Given:
We have to draw a $\Delta ABC$ in which AB = 47 cm, AC = 47 cm and $\angle BAC={{75}^{0}}$ .
Now, before we proceed we should know how to draw an angle of ${{75}^{0}}$ and bisect it, and how to draw perpendicular bisector of any line segment.
Follow following steps to draw $\angle BAC={{75}^{0}}$ and its angular bisector:
1. Draw a segment of length 47 cm and name it AB. The figure is shown below:

2. Now, draw an arc of certain radius less than 47 cm with centre at point A as shown in the figure below:

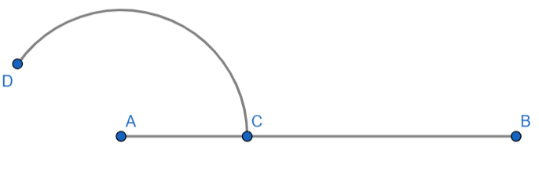
3. Now, draw an arc of the same radius with centre at point C and make it intersect the previous one at point G. The figure is shown below:

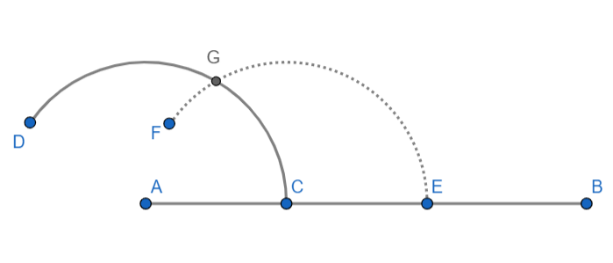
4. Now, draw an arc of same radius with centre at point G and make it intersect the previous one at point J. The figure is shown below:

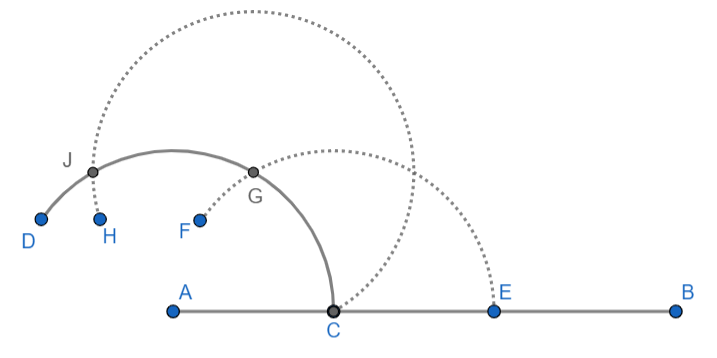
5. Now, draw an arc of same radius with centre at point J and make it intersect the previous one at point L and join AL and segment AL will intersect the arc CD at point M. The figure is shown below:

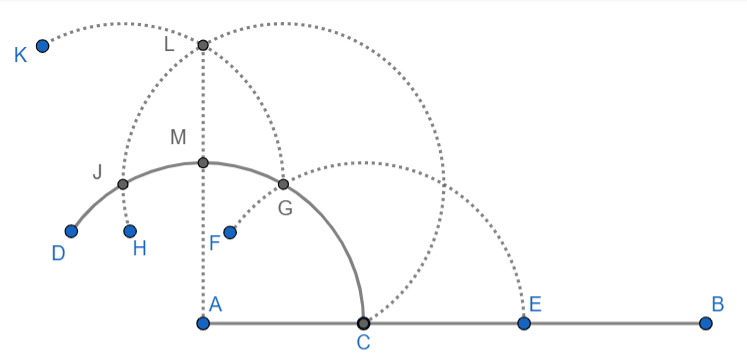
6. Now, draw an arc of same radius with centre at point M and make it intersect the arc CH at point O and join AO and make it intersect the arc CD at point P. The figure is shown below:

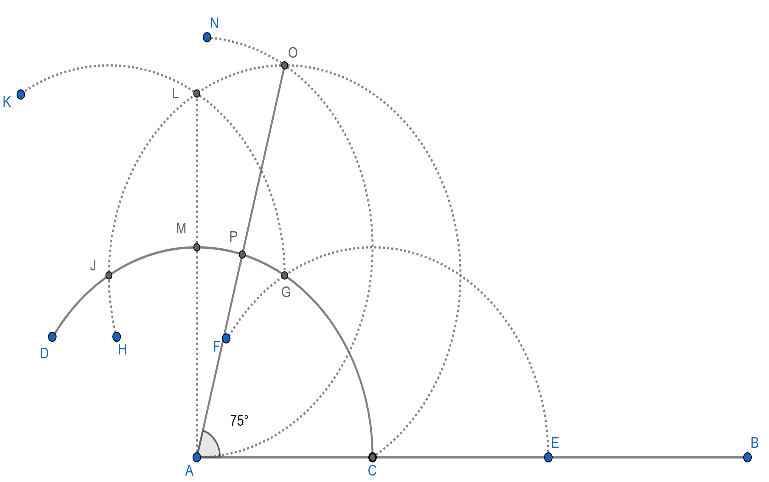
7. Now, $\angle OAB$ is the required angle of ${{75}^{0}}$ .
8. Now, we will bisect $\angle OAB$ . First, draw an arc of the same radius with centre at point P and make it intersect the arc EF at point R and join AR. The figure is shown below:

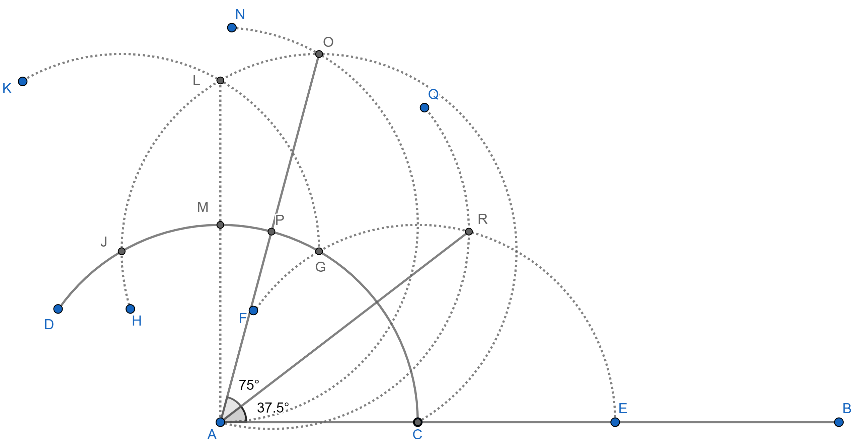
9. Now, AR is the required angular bisector of the $\angle OAB$ .
Now, we will see how to draw the perpendicular bisector of any line segment.
Follow the following steps to draw perpendicular bisector of any line segment:
1. Let there be a line AB of certain length as shown in the figure below:

2. Now, draw an arc of radius more than half length of the segment AB with centre A on the above and below of the segment as shown in the figure below:

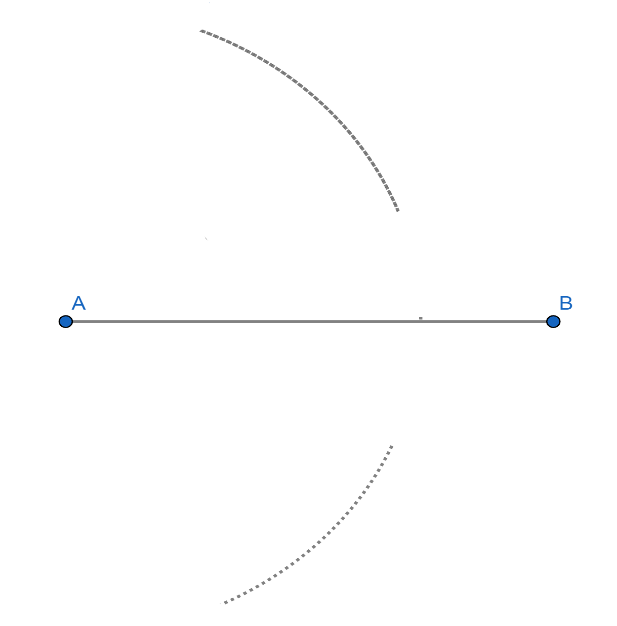
3. Now, draw an arc of same radius with centre B on the above and below of the segment and make it intersect the previous two arcs as shown in the figure below:

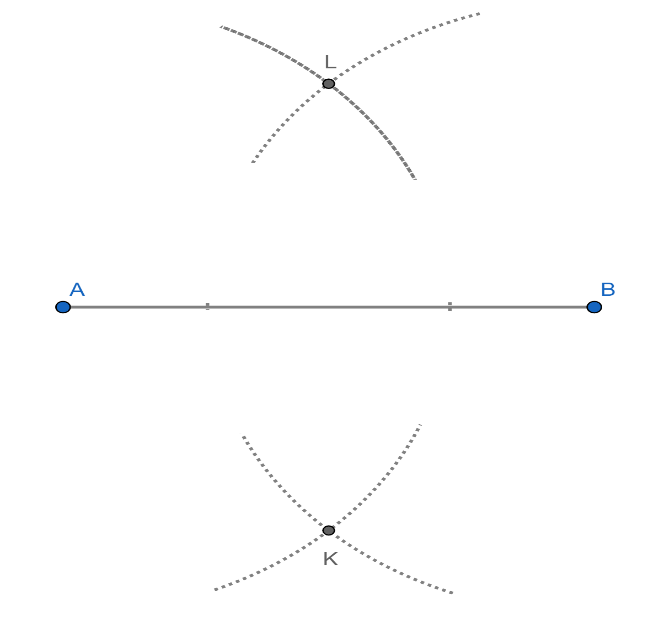
4. Now, join the point K and point L as shown in the figure below:

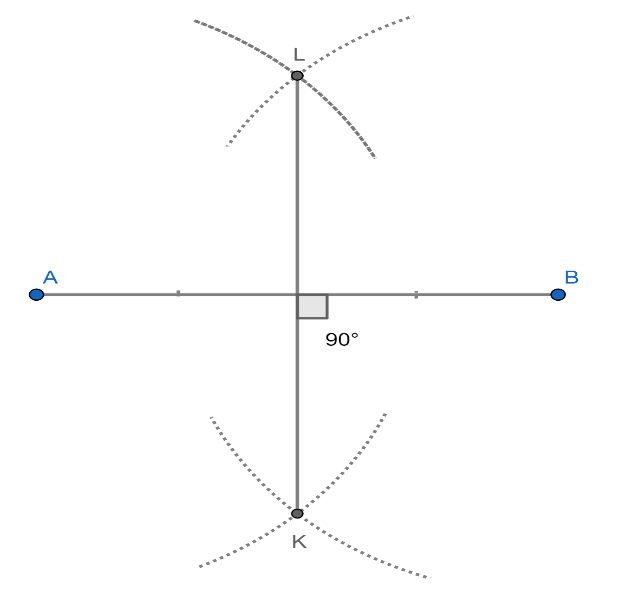
5. Now, KL is the required perpendicular bisector of the line segment AB.
Now, we will use these methods to draw the diagram as per the given data. Follow the following steps to draw the required $\Delta ABC$ :
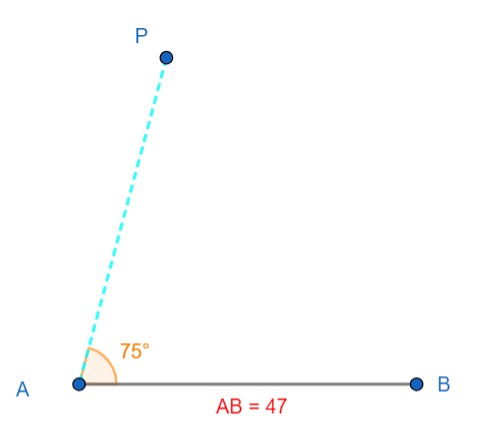
1. Draw a segment of length 47 cm and name it AB. The figure is shown below:

2. Now, with the help of compass draw an angle of 75 degrees as shown in the figure below:

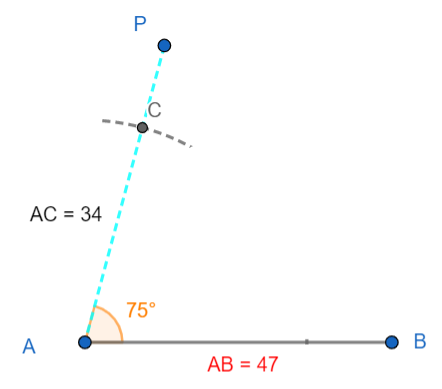
3. Now, on the segment AP mark point C such that AC = 34 cm as shown in the figure below:

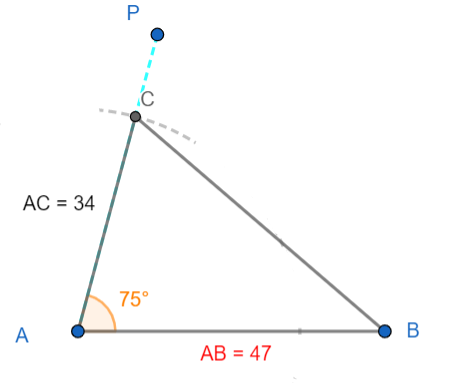
4. Now, join the point A and C, point B and C to get the $\Delta ABC$ as shown in the figure below:

5. Now, draw the angle bisector AD of the $\angle BAC$ as shown in the figure below:

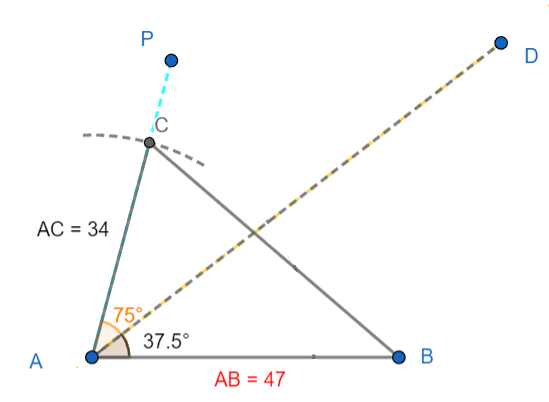
6. Now, draw the perpendicular bisector of the BC to get the point M as per the given data. The figure is shown below:

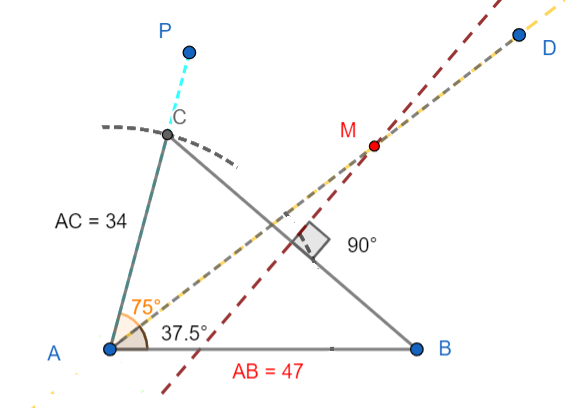
7. Now, join the point C and M to get CM and point B and M to get BM. Then, measure $\angle BMC$ . The figure is given below:

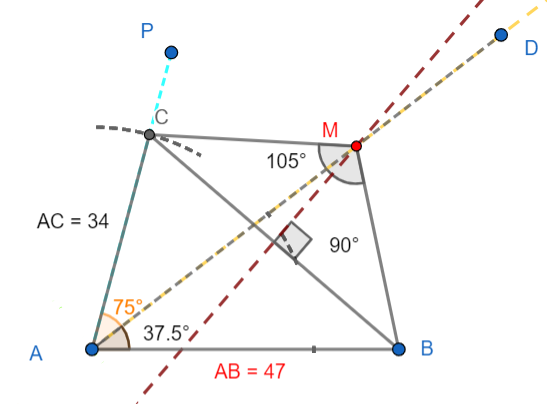
8. Now, as shown in the above figure that $\angle BMC={{105}^{0}}$ .
Thus, $\angle BMC={{105}^{0}}$ .

Note: Here, the student must draw the diagram neatly and correctly. Moreover, while drawing the diagram students should be aware of what is asked in the question and proceed as per the instructions given to get the correct answer.