Question

What is the value for $ y $ ? Explain how you arrived at your answer.

Answer 1

Hint: For solving this particular question you have to use angle sum property of a triangle, and the isosceles triangle property that is in an isosceles triangle angles two sides are equal to each other. The third unequal side of an isosceles triangle is termed the base of the isosceles triangle. The two angles opposite to the equal sides are equal to each other.

Complete step by step solution:
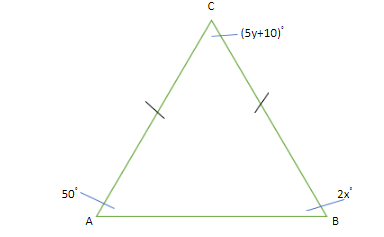
It is given that ABC is a triangle ,
Where ,
 $ \angle A = {50^ \circ } $ , it is given in the figure ,
 $ \angle B = 2{x^ \circ } $ , again, from the figure,
 $ \angle C = {(5y + 10)^ \circ } $ , again, from the figure,
It is also given it is an isosceles triangle that is $ \overline {AC} = \overline {BC} $ ,
We know that in an isosceles triangle angles two sides are equal to each other. The third unequal side of an isosceles triangle is termed the base of the isosceles triangle. The two angles opposite to the equal sides are equal to each other.
By keeping this property in mind, we get the following result ,
 $
   \Rightarrow {50^ \circ } = 2{x^ \circ } \\
   \Rightarrow {25^ \circ } = {x^ \circ } \;
  $
Here we get the value of $ x = 25{}^ \circ $ ,
Now, we know that in a triangle sum of all three interior angles is equal to $ {180^ \circ } $ ,
Therefore, we can write as follow ,
\[ \Rightarrow \angle A + \angle B + \angle C = {180^ \circ }\] ( angle sum property of a triangle)
Now, substitute the values , we will get the following result,
 $ \Rightarrow 50{}^ \circ + 2x{}^ \circ + (5y + 10){}^ \circ = 180{}^ \circ $
Now, substitute the value of $ x = 25{}^ \circ $ in the above equation,
 $ \Rightarrow 50{}^ \circ + 50{}^ \circ + (5y + 10){}^ \circ = 180{}^ \circ $
Simplifying the above equation ,we will get ,
 $ \Rightarrow 100{}^ \circ + (5y + 10){}^ \circ = 180{}^ \circ $
Subtract $ 100{}^ \circ $ from both the side of the equation , we will get ,
 $ \Rightarrow (5y + 10){}^ \circ = 80{}^ \circ $
Subtract $ 10{}^ \circ $ from both the side of the equation , we will get ,
 $ \Rightarrow (5y){}^ \circ = 70{}^ \circ $
Divide the equation by $ 5 $ to both the side, we will get ,
 $ \Rightarrow y{}^ \circ = 14{}^ \circ $
Here we get the required result.
So, the correct answer is “ $ y{}^ \circ = 14{}^ \circ $ ”.

Note: The mathematical operations such as addition, subtraction, multiplication and division is used. Use addition or subtraction properties of equality to gather variable terms on one side of the equation and constant on the other side of the equation. Use the multiplication or division properties of equality to form the coefficient of the variable term equivalent to one.