
Value of Gravitational Constant ‘G’ is
Answer
499.5k+ views
Hint: Gravitational Constant is the universal constant and one should memorize its value but in case you have forgotten that value. Then find the formula through which we can find the value of the gravitational constant one of the formula is
Formula used:
Gravitational Force between two objects, one of Mass
Where,
Also,
Complete step by step answer:
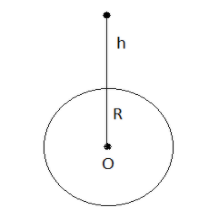
To determine the value of the gravitational constant, firstly, let us place an object of mass
Here,
If the object of mass
Also, acceleration is given as force divided by mass i.e.
Therefore acceleration due to gravity is the gravitational force divided by the mass of the object.
But,
Or,
Hence, option A is correct.
Note:
We must know that gravitational force is one of the weakest forces in nature. The Gravitational constant remains as a constant everywhere. Although acceleration due to gravity changes with altitude, depth, and rotation of earth but Gravitational constant never changes. If we compare the electrostatic force and gravitational force, we can find that gravitational force is
Formula used:
Gravitational Force between two objects, one of Mass
Where,
Also,
Complete step by step answer:

To determine the value of the gravitational constant, firstly, let us place an object of mass
Here,
If the object of mass
Also, acceleration is given as force divided by mass i.e.
Therefore acceleration due to gravity is the gravitational force divided by the mass of the object.
But,
Or,
Hence, option A is correct.
Note:
We must know that gravitational force is one of the weakest forces in nature. The Gravitational constant remains as a constant everywhere. Although acceleration due to gravity changes with altitude, depth, and rotation of earth but Gravitational constant never changes. If we compare the electrostatic force and gravitational force, we can find that gravitational force is
Recently Updated Pages
Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Master Class 9 English: Engaging Questions & Answers for Success

Master Class 9 Science: Engaging Questions & Answers for Success

Master Class 9 Social Science: Engaging Questions & Answers for Success

Master Class 9 Maths: Engaging Questions & Answers for Success

Class 9 Question and Answer - Your Ultimate Solutions Guide

Trending doubts
State and prove Bernoullis theorem class 11 physics CBSE

Who built the Grand Trunk Road AChandragupta Maurya class 11 social science CBSE

1 ton equals to A 100 kg B 1000 kg C 10 kg D 10000 class 11 physics CBSE

State the laws of reflection of light

One Metric ton is equal to kg A 10000 B 1000 C 100 class 11 physics CBSE

Difference Between Prokaryotic Cells and Eukaryotic Cells




