Question

What is the velocity of efflux? Derive the expression for the velocity of efflux from the side of the container when its top is open to the atmosphere.

Answer 1

Hint: This question requires the knowledge of fluid mechanics. This problem is based upon the topic of velocity of efflux. The velocity of efflux is the velocity with which a liquid will come out of a hole carved at some height from the bottom of the container in which the liquid is filled.

Complete step by step answer:
Consider a liquid-filled tank (e.g. water tank). At some point in time, there should be a hole in the tank's wall at a depth h from the fluid's free surface in the open tank. The tank's cross section area, A, is much larger than the hole's cross section area, a. (A>>>a)
The efflux velocity, $v_e$, is the rate at which the fluid emerges from the hole.

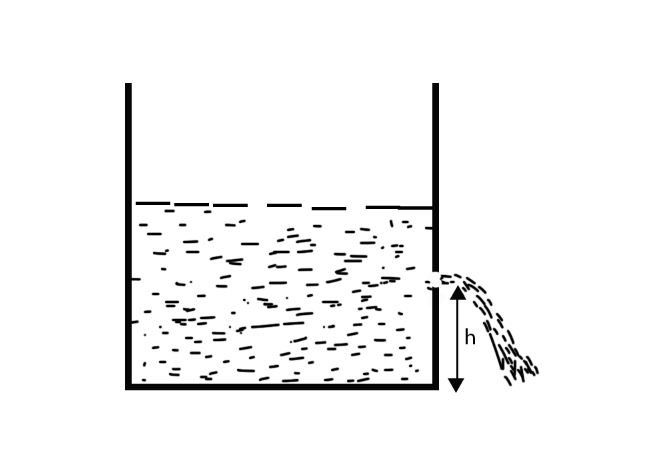
Let $v_e$ be the velocity with which the fluid leaves. $v_g$, velocity at ground will be zero.
$g$ be acceleration due to gravity and $h$be the height from which fluid falls.
So according to equation of motion,
${v_g}^2={v_e}^2+2gh$
Since water is flowing downwards, we take $h$ as negative.
$0={v_e}^2-2gh$
$v_e=\sqrt{2gh}$
This is the expression for velocity of efflux.

Note: The velocity of efflux is independent of the nature of liquid, quantity of liquid in the vessel and the area of orifice. More the height of the hole from the surface, more will be the velocity of efflux. The velocity of efflux of a liquid is the same as the speed an object would acquire while falling from the same height.